An image of Heer de Beer

Heer de Beer.org

Exploring the Computational Medium

Virtual botanical laboratory

Huub de Beer

October 2017

1 Chapter 1. Introduction

A while back I was reading Artificial life. A report from the frontier where computers meet biology (Levy, 1992). In this book, Levy describes the development of the scientific field of artificial life till the 1990s. Although I think the book was less readable than his work Hackers (Levy, 2010), it was still an interesting read. What piqued my interest most in Levy’s book on artificial life was the idea of generating plant-like structures by means of a rewriting system known as an L-system.

In the notes to the Chapter Artificial flora, artifical fauna, artificial ecologies I found a reference to a book called The algorithmic beauty of plants (Prusinkiewicz & Lindenmayer, 1990). Given its age, I had little hope in finding this book. To my surprise, it is available on-line! (Warning, this is a 17Mb PDF; see http://algorithmicbotany.org/papers/#abop for smaller versions.)

I downloaded the book and started reading it. Chapter 1 is introductory material introducing the L-system formalism, its extensions, and a way to render these L-systems. The authors render the L-systems by interpreting it in terms of turtle graphics. Turtle graphics is quite a simple way of thinking about drawing things with a computer: given a turtle holding a pen, tell the turtle where to move, to rotate, and to push the pen to the paper or not.

Seeing the turtle interpretation, I tried to read (Prusinkiewicz & Lindenmayer, 1990) using a constructionist approach by building the examples myself. After a couple of fun hours programming these prototypes, I decided to write my own virtual botanical laboratory because I assumed that the software described in The algorithmic beauty of plants would not exist anymore. Later, when I had finished most of the engine of my virtual botanical laboratory, I discovered that the group who put the book on-line also have put their software on-line as well.

Figure 1.1 How much fun: I generated an odd looking tree!
How much fun: I generated an odd looking tree!

Then again, building my own laboratory probably deepened my understanding of the material I would not have reached by using the available software. Here I present my own virtual botanical laboratory that I unoriginally named virtual_botanical_laboratory. Feel free to use is to explore the book The algorithmic beauty of plants yourself, use it to generate your own plant-like shapes, or just have fun with it! (For example, look at that odd looking tree I generated above :-))

In the next Chapter, the virtual_botanical_laboratory is introduced by enumerating the examples from Chapter 1 of The algorithmic beauty of plants defined in the virtual_botanical_laboratory. After that introduction, the use of the software a description of the user interface, followed by 2) an overview of the L-system language. Finally, building the software is discussed, including a list with to do items.

1.1 1.1 Example

A simple growing weed of sorts. From: Prusinkiewicz and Lindenmayer (1990) The Algorithmic Beauty of Plants, p.25, Figure 1.24

How to run this example on your own is explained in the next section.

1.2 1.2 Running the virtual_botanical_laboratory

To run the virtual_botanical_laboratory, you need to:

For more examples, please see the examples.

For more information about creating and configuring L-systems, see the chapters below.

1.3 1.3 License

virtual_botanical_laboratory is free software; virtual_botanical_laboratory is released under the GPLv3. You find virtual_botanical_laboratory’s source code on github.

2 Chapter 2. Reading The algorithmic beauty of plants

In this Chapter all examples in the first Chapter of the book The algorithmic beauty of plants, Graphical modeling using L-systems, are recreated using the virtual_botanical_laboratory. I recommend you read the book’s chapter while exploring the examples. In doing so, you will get familiar with the syntax of defining a L-system.

Note. Sometimes doing another derivation might crash your browser.

3 Chapter 3. Using the virtual botanical laboratory

3.1 3.1 Interface

The virtual_botanical_laboratory has a very simple and bare-bones user interface. It has been added more as an afterthought than that it has been designed with user experience in mind. (Feel free to create a better interface, virtual_botanical_laboratory is free software after all.)

The interface is meant to show the generated images while giving the user access to the underlying L-system and the configuration of the interpretation of that L-system.

The user interface consists of five tab pages:

  1. On the main tab page, labeled with ♣, you can see the rendered L-system (see figure below). It also has some buttons to control the L-system and export the rendering.

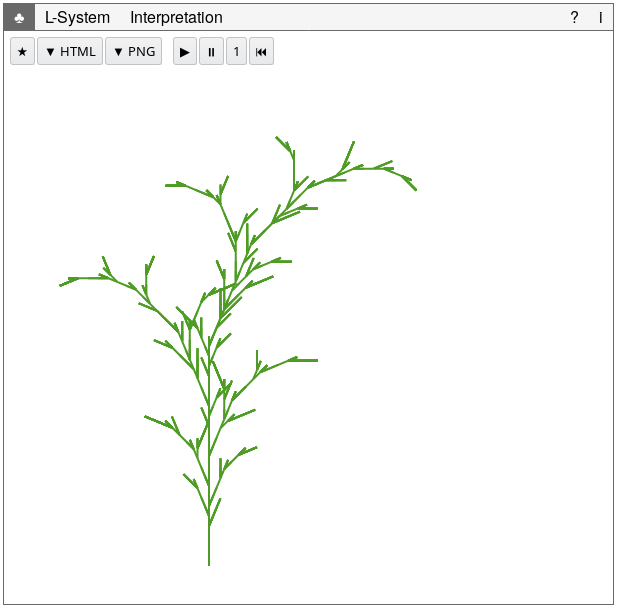
    Figure 3.1 The main tab to view and control the L-system
    The main tab to view and control the L-system

    The following “file” actions are available:

    • ★ (New): create a new empty virtual botanical laboratory in a new window.
    • ▼ HTML (Export to HTML): export the virtual botanical laboratory to a HTML file. By default, this file is named after the L-system.
    • ▼ PNG (Export to PNG): export the rendered L-system to a PNG file. By default, this file is named after the L-system.

    The following “control” actions are available:

    • ▶️ (Run): derive new successors for the L-system until it has reached the derivation length set by property derivationLength. You can set that option on the Interpretation tab.
    • ⏸ (Pause): stop deriving new successor.
    • 1 (Step): derive the next successor for the L-system. Note. Due to the inefficiencies with respect to memory, this might crash your browser.
    • ⏮ (Reset): reset the L-system to the axiom.

  2. You can view and edit the L-system definition on the L-system tab (see figure below).

    Figure 3.2 The L-system tab to view and change the L-system’s definition
    The L-system tab to view and change the L-system’s definition

    When you change the L-system, press the Update button to have the changes take effect. This will parse the L-system’s definition. If you make an error, a warning is displayed. If everything is okay, a temporary information message to that effect is shown. Switch back to the main tab to see the changes in action.

  3. You can view and change the configuration of the interpretation on the Interpretation tab (see figure below).

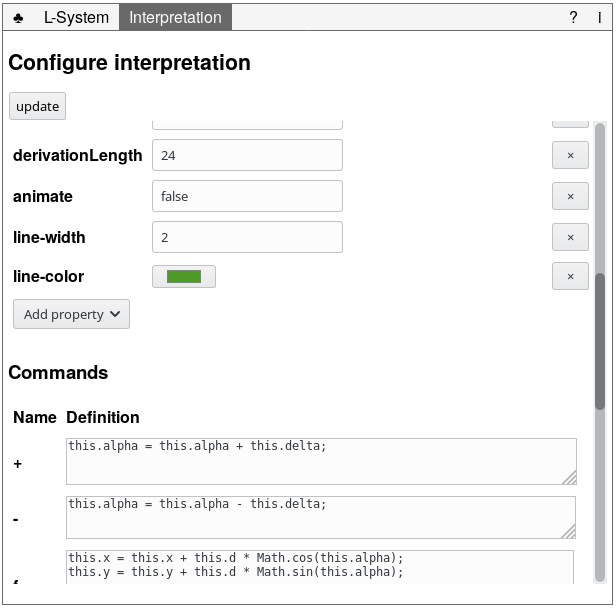
    Figure 3.3 The Interpretation tab to view and change the L-system’s interpretation
    The Interpretation tab to view and change the L-system’s interpretation

    On this Interpretation tab, there are two sections:

    1. Properties, which is an editable list of properties you can set, update, or remove. These properties include:

      • the width and height of the canvas
      • the start coordinates x, y
      • the start angle alpha
      • the distance to draw each F command, d
      • the rotation to apply each + and - command, delta
      • the close property to connect start and end points
      • the derivationLength property to set the number or derivation steps to perform
      • the animate property to indicate if each derivation step has to be shown or only the final result
      • the line-width
      • the line-color

    2. Commands, which is a list of all commands defined in the L-system. You can edit their definitions. Note. the this refers to the [Interpretation](https://heerdebeer.org/Software/virtual_botanical_laboratory/documentation/api/Interpretation.html).

      The commands F, f, +, and - are defined by default. If you want to change their behavior, you have to introduce a new symbol in the L-system and write its command’s code. You can call the default implementation as follows:

      this.getCommand("F").execute(this);

  4. You can read a short manual on the Help tab (labeled ?).

  5. You can read about the virtual_botanical_laboratory and its license on the About tab (labeled i).

3.2 3.2 The L-system language

The language to define a L-system follows the language described in the (first chapter of the) book The algorithmic beauty of plants (Prusinkiewicz & Lindenmayer, 1990). There are some notable differences:

  1. Symbol names should be separated from each other. If you want to denote an F followed by another F, write F F rather than FF.
  2. Symbols can have names of any length larger than 0. So you can use symbol Forward instead of F if you so please.
  3. 3D aspects of the language have not yet been implemented.
  4. Language features described outside of Chapter 1 of Prusinkiewicz & Lindenmayer (1990) have not yet been implemented.

Next the features of the L-system definition language are briefly introduced. For a more thorough overview, please see the Chapter on reading Prusinkiewicz & Lindenmayer (1990).

3.2.1 Basic L-system definitions

A basic L-system is defined by three parts:

  1. An alphabet with symbols, such as F, -, and +.
  2. The axiom or the initial string of symbols, such as F F.
  3. A list of rewriting rules called productions, such as F -> - F + F.

You specify the above L-system as follows:

my_first_lsystem = lsystem(
    alphabet: {F, -, +},
    axiom: F F,
    productions: {
        F -> - F + F,
        - -> -,
        + -> +
    }
)

Identity rewriting rules like + -> + can be omitted. If there is no rewriting rule specified for a symbol in the language, the identity rewriting rule is used by default.

For documenting purposes, you can also add a description to the L-system definition. So, the above example can be rewritten as:

my_first_lsystem = lsystem(
    description: "This is my first L-system definition!",
    alphabet: {F, -, +},
    axiom: F F,
    productions: {
        F -> - F + F
    }
)

One of the interesting features of L-systems are branching structures. To define a sub structure, place it in between [ and ]. For example:

expanding_tree_circle = lsystem(
    alphabet: {F, -, +},
    axiom: F,
    productions: {
        F -> F [ + F] - F
    }
)

This will generate some expanding circle of branching lines.

3.2.2 Extensions to the L-system definition language

4 Chapter 4. Developing virtual_botanical_laboratory

Note. The virtual_botanical_laboratory is quite SPACE inefficient. This is fine for the prototype it is now, but this issue needs to be addressed when continuing the project.

If you plan on extending or adapting the virtual_botanical_laboratory, see the API documentation.

4.1 4.1 Building

4.2 4.2 Todo

The virtual_botanical_laboratory is still a work in progress. With the current version you can explore much of the material in the book The algorithmic beauty of plants (Prusinkiewicz & Lindenmayer, 1990). Some more advanced features from later in that book needs to be implemented still.

The following list of features and improvements are still to do:

Chapter 5. References

Levy, S. (1992). Artificial life. A report from the frontier where computers meet biology. New York: Vintage books.
Levy, S. (2010). Hackers. Sebastopol: O’Reilly.
Prusinkiewicz, P., & Lindenmayer, A. (1990). The algorithmic beauty of plants. New York: Springer-Verlag. Retrieved from http://algorithmicbotany.org/papers/#abop