Rekenmachines en programmeren op het MC
Huub de Beer
Amsterdam, 26 februari 2008
1 Inleiding
In de jaren ’50 van de vorige eeuw bouwde en gebruikte de Rekenafdeling van het Mathematisch Centrum (MC) in Amsterdam verschillende automatische rekenautomaten. Tussen 1951 en 1956 werden vier machines ontworpen, gebouwd en gebruikt. De in deze tijd opgedane kennis en ervaring op het gebied van computers werd veiliggesteld en uitgebreid door de oprichting van een computerfabriek door de Nillmij: Electrologica. De Rekenafdeling leverde de kennis, de Nillmij de financiering; het resultaat was de X1, de eerste werd in 1958 geleverd aan de Nillmij in Den Haag.
Over de geschiedenis van de computerbouw op het MC is al veel geschreven. Vaak zijn dit verhalen met een anekdotische inslag: leuk om te lezen, maar de beschreven machines blijven curieuze objecten. Onduidelijk is hoe deze rekenmachines gebruikt werden, onduidelijk is hoe ze precies gebouwd werden of wat men aan het MC eigenlijk verwachtte van deze machines.
Om dergelijke vragen te beantwoorden zijn bronnen nodig die juist dit gebruiksaspect behandelen. Helaas zijn die bronnen schaars. In de anekdotische verhalen komen dergelijke aspecten amper naar voren, anders dan in uitzonderlijke situaties. Van de programma’s die geschreven en gedraaid zijn en het ontwikkelingsproces is niets bewaard. Wat rest zijn een groot aantal technische rapporten over de verschillende machines, over enige superprogramma’s en een aantal cursussen programmeren voor automatische rekenmachines.
Deze rapporten bieden aan de ene kant een schat aan technische details waaruit veel af te leiden over het gebruik van de computers van de Rekenafdeling. Aan de andere kant zijn het rapporten die vaak aangeven wat men wil met een bepaalde machine, of het zijn beschrijvingen van een aantal belangrijke subroutines dan wel superprogramma’s. Dat wil zeggen dat het gebruik op gebruikersniveau amper aan bod komt; er worden wel aanwijzingen gegeven hoe te programmeren of hoe de computer gebruikt zou moeten worden, maar van het daadwerkelijk gebruik is, zoals eerder gezegd, geen directe informatie.
Omdat de rapporten een serie van machines beschrijven op min of meer vergelijkbare manier is het echter wel mogelijk om de ontwikkeling die men op de Rekenafdeling heeft doorgemaakt in zowel machinebouw, programmeren en documentatie te onderzoeken. En juist deze ontwikkeling geeft informatie over hoe de computers werden gebruikt op de Rekenafdeling van het MC.
Hierna worden achtereenvolgens de rapporten over de verschillende computers en het gebruik ervan beschreven. Het doel is om de ontwikkeling in zowel computerbouw als computergebruik aan te geven en deze ontwikkeling wordt in de conclusie nog eens kort gekenschetst.
2 ARRA (I)
De eerste computer die aan het MC gebouwd werd was de ARRA. Van deze machine is weinig bekend, in de jaarverslagen van het MC komt niet naar voren dat de machine een belangrijke rol speelde bij de rekenopdrachten die de Rekenafdeling uitvoerde. Zeker, de machine is gestest en er zijn enkele tabellen gemaakt. Of de machine voor andere problemen is ingezet is onduidelijk.
Over deze machine is een rapport gemaakt: Programmeren voor de A.R.R.A.1 geschreven door het hoofd van de Rekenafdeling, Aad van Wijngaarden, in 1951. In dit rapport wordt ‘de theorie van de programmering behandeld voor het stadium, waarin de machine het eerst gebracht zal worden na de ombouw volgend op het eerste stadium van gebruik in 1950.’2 Met andere woorden, de machine is nog in ontwikkeling, maar dit document beschrijft hoe Van Wijngaarden de uiteindelijke machine en het gebruik ervan ziet.
Ondanks de titel van het rapport is het geen cursus programmeren voor de ARRA, het is meer een technisch handboek voor het gebruik van de ARRA. Het begint met de introductie van automatische digitale machines: de verschillende onderdelen van zo’n machine, zoals geheugen, besturing, rekenorgaan, invoer en uitvoer, komen achtereenvolgens aan bod.
De ARRA kent 16 opdrachten (zie hieronder), die niet allemaal tegelijk geïntroduceerd worden. Van Wijngaarden begint met eenvoudige operaties en geeft meteen enkele voorbeeld programmatjes, het belang van de sprongopdracht wordt opgemerkt. Een ander belangrijk aspect is dat woorden zowel getallen als opdrachten kunnen zijn en dat opdrachten in feite ook als getal geïnterpreteerd kunnen worden en zo aangepast. Hiermee kunnen complexe programma’s gemaakt worden.
| 0,n | Telt (n) op bij (A). |
| 1,n | Plaatst (n) in S. |
| 2,n | Schrijft (A) op adres n. |
| 3,n | Schrijft (S) op adres n en in A. |
| 4,n | Vormt (n) \(\times\) (S) \(+\) p \(\times\) (A) en plaatst het resultaat in A en S. |
| 5,n | Vormt (n) \(\times\) (S) \(+\) \(\frac{1}{2}\) p en plaatst het resultaat in A en S. |
| 6,n | Vermenigvuldigt (A) met \(2^n\). |
| 7,n | Verplaatst besturing naar n als (A) \(\geq\) 0. |
| 8,n | Trekt (n) af van (A). |
| 9,n | Communicatieopdracht. |
| 10,n | Schrijft (A) op adres n en maakt A schoon. |
| 11,n | Schrijft (S) op adres n en maakt A schoon. |
| 12,n | Deelt (A) \(+\) p \(\times\) (S) door (n), plaatst rest in A en quotient in S. |
| 13,n | Deelt (A) door (n), plaatst afgerond quotient in S en maakt A schoon. |
| 14,n | Vermenigvuldigt (A) met \(2^{-n}\). |
| 15,n | Verplaatst besturing naar n als (A) \(<\) 0. |
Programma’s worden op een speciale manier genoteerd: in principe is het een lijst van opeenvolgende paren van adres en opdracht. Een opdracht wordt aangegeven door opdrachtnummer en adres waar het betrekking op heeft gescheiden door een schuine streep. Daarnaast worden door middel van pijlen aangegeven waar een sprongopdracht binnenkomt en vertrekt. Een dubbele pijl betekend dat een sprong onvoorwaardelijk is. Bij binnenkomende pijlen wordt ook het adres van waar gesprongen word genoteerd.
Na deze korte introductie van de rekenmachine gaat Van Wijngaarden dieper in op de technische details van de ARRA. Het is een binaire machine met woorden van 30 cijfers. Bit 0 is het tekenbit en door inversie van alle binaire cijfers kan van een positief getal een negatief getal gemaakt worden. In een adres is dus plaats voor getallen tussen plus en min 536870911. Naast gehele getallen zijn er ook breuken. In dat geval wordt tussen het eerste en tweede cijfer van een woord de komma gelezen.
Invoer en uitvoer is een belangrijk onderdeel van de machine. De ARRA beschikt over een schrijfmachine waarop 16 verschillende handelingen kunnen worden uitgevoerd: het afdrukken van de getallen 0 tot en met 9, \(+\), \(-\), ‘.’, tabulatie, spatie en ‘terugwagen, nieuwe regel’. Er kan zowel imperatief als facultatief getypt worden. Bij facultatief typen worden extra nullen voor een geheel getal niet afgedrukt maar vervangen door een spatie.
Het besturen van de typemachine gebeurt met opdracht 9 en een adres dat een code voorsteld. De code specificeert of er een breuk of geheel getal moet worden afgedrukt en hoeveel plaatsen voor en na de komma van een breuk afgedrukt moet worden. Deze codes staan op een geblokkeerd kanaal in het geheugen
Naast uitvoer via de typemachine is er ook invoer via een ponsbandlezer. In het geblokkeerde geheugen bevindt zich een invoerprogramma dat het lezen van de band mogelijk maakt. Dit ionvoerprogramma maakt de vertaling van de pentades ingegeven op de ponsmachine naar getallen en opdrachten op de juiste plaats in de machine. Door middel van speciale eindletters die door de gebruiker een waarde gegeven moet worden, kan eenvoudig een reeks opdrachten of getallen op een bepaalde plaats in het geheugen gezet worden.
Voor het ponsen van een programma zijn speciale formulieren. De programmacode die de programmeur ingeeft is dus anders dan de uiteindelijke machinecode. op de ponsband kan het begin en einde gemarkeert worden door een groot aantal correctietekens (dat zijn vijf gaatjes) en spaties (dat zijn nul gaatjes) te ponsen. Het invoerprogramma zelf wordt ook besproken in het volgende hoofdstuk en bestaat uit 50 opdrachten.
Hierna komen subroutines aan bod. Bij een subroutineaanroep wordt het terugkeer adres in A geplaatst dat door de subroutine in een sprongopdracht aan het einde van de routine geplaatst wordt. Het ponsen van subroutines komt ook nog het zogenaamde voorponsen bij.
Al met al is dit rapport een summiere handleiding van het gebruik van de ARRA. Echt handig of duidelijk is het allemaal niet beschreven, maar het zal voor deze ARRA zeker wel voldaan hebben: de machine zelf was ook verre van uitontwikkeld.
3 ARRA (II)
In 1952 werd besloten een opvolger voor de ARRA te bouwen, de ARRA (II). Over deze machine zijn vier rapporten verschenen, alle van de hand van Edsger Dijkstra die in 1952 aangenomen was bij de Rekenafdeling als programmeur. In 1954 werd de ARRA in gebruik genomen en werd tot en met 1956 ingezet voor verschillende rekenopdrachten.3 Het eerste rapport over de ARRA II is geschreven in 1953, de volgende twee in 1954. Met andere woorden, ook hier werd de beschrijving van de machine en de bouw van de machine tegelijkertijd uitgevoerd: deze rapporten, zeker het eerste, beschrijft dus hoe de machine zou moeten worden.
Het Functionele beschrijving van de ARRA4 uit 1953 lijkt in sommige opzichten op de eerdere beschrijving van de ARRA I. Aan de andere kant is dit rapport duidelijk een stap verder dan het vorige. Zo introduceert Dijkstra extra notatie om de interpretatie van woorden aan te geven. Een woord op adres n wordt aangegeven met (n) als een algemeen woord geïnterpreteerd wordt. Het wordt met [n] aangegeven als het een geheel getal betreft en met n als het een breuk betreft. Verder is er de notatie <n> dat geïnterpreteerd moet worden als een opdrachtenkoppel.
| 0/n | vervang (A) door (A)\(+\)(n) |
| 1/n | vervang (A) door (A)\(-\)(n) |
| 2/n | vervang (A) door (n) |
| 3/n | vervang (A) door \(-\)(n) |
| 4/n | vervang (n) door (A) |
| 5/n | vervang (n) door \(-\)(A) |
| 6/n | conditionele besturingsverplaatsing naar n a |
| 7/n | besturingsverplaatsing naar n a |
| 8/n | vervang (S) door (S)\(+\)(n) |
| 9/n | vervang (S) door (S)\(-\)(n) |
| 10/n | vervang (S) door (n) |
| 11/n | vervang (S) door \(-\)(n) |
| 12/n | vervang (n) door (S) |
| 13/n | vervang (n) door \(-\)(S) |
| 14/n | conditionele besturingsverplaatsing naar n b |
| 15/n | besturingsverplaatsing naar n b |
| 16/n | vervang [AS] door [n].[s] \(+\) [A] |
| 17/n | vervang [AS] door -[n].[s] \(+\) [A] |
| 18/n | vervang [AS] door [n].[s] |
| 19/n | vervang [AS] door -[n].[s] |
| 20/n | deel [AS] door [n], plaats quotient in S, rest in A |
| 21/n | deel [AS] door -[n], plaats quotient in S, rest in A |
| 22/n | “Schuif A\(\rightarrow\)S”, d.w.z. vervang [AS] door [A].\(2^{29-n}\) |
| 23/n | “Schuif S\(\rightarrow\)A”, d.w.z. vervang [SA] door [S].\(2^{30-n}\) |
| 24/n | communicatie opdracht |
De nieuwe ARRA kent 25 opdrachten en het is meteen al duidelijk dat de ARRA II een meer doordachte machine is dan de ARRA I. De opdrachten met betrekking op A en S zijn dubbel uitgevoerd en netjes gegroepeerd. Voor het gebruik van subroutines zijn nu onconditionele besturingsverplaatsingen toegevoegd. De ARRA is een 30 bits machine en in elk woord passen twee opdrachten: een a en een b opdracht. Aan de ene kant is dit onhandig omdat er extra administratie door de machine moet worden uitgevoerd, maar aan de andere kant is het wel efficiënter in het geheugengebruik: elke opdracht is dus 15 bits lang, 5 bits voor de opdracht en 10 bits voor het adres waarmee dus 1024 geheugenplaatsen bereikt kunnen worden, precies de grootte van het geheugen.
Relatief veel aandacht wordt besteed aan de communicatie van de machine met de buitenwereld via opdracht 24. Naast het communiceren met ponsbandlezer en typemachine zijn ook special handelingen via deze opdracht beschikbaar via een code in plaats van een adres. Onder deze handelingen valt ook de communicatie met de console.
Hierna komt een hoofdstuk over de snelheid van de opdrachten, waarin uitgelegd wordt dat de wachttijd van het geheugen de beperkende factor is en dat door handig om te gaan met het plaatsen van gegevens de tijdsduur van een opdracht verkort kan worden. Het trommelgeheugen bestaat uit 64 kanalen (gelezen en beschreven door 64 koppen) die elk 16 woorden bevatten.
De machine moet via de bedieningstafel bediend worden. Op die tafel zijn de ponsbandlezer, de schrijfmachine, 2 oscillografen, het schakelaarspaneel en het toetsenpaneel. De rechterhelft van het toetsenpaneel is het handregister (14 toetsen) waarmee getallen in het register S gebracht kunnen worden. Met behulp van het schakelaarspaneel, bestaande uit 4 rijen schakelaars, kan een getal ingezet worden. Met de onderste rij schakelaars kan een getal in A gelezen worden met opdracht 24/7. De andere rijen schakelaars zijn bedoeld voor “begin adres”, “stop adres” en “opdracht”, deze worden gebruikt om operaties ingegeven op de linkerhelft van het toetsenpaneel te specificeren. Met andere woorden, via de console kan het programma dat de machine draait gemanipuleerd worden
Op de ponsmachine zijn 32 toetsen, een zestal sluitlettertoetsen, A, A, B, C, D, E, F, waarvan de vier laatste ook tekentoetsen zijn en nog 24 getaltoetsen, van 0 tot en met 24.
In de eerste vijf kanalen van het geheugen is het invoerprogramma aanwezig dat zowel het toetsenpaneel als de ponsband bestuurt. Dit programma beslaat 78 woorden, waarvan er 13 als werkruimte zijn bestempeld. Dit zijn dus 130 opdrachten, bijna drie keer zo veel als van de ARRA I.
Hierna komt een hoofdstuk met de titel ‘De taak van de programmeur’:
De specifieke taak van de programmeur is een onderdeel van de voorbereiding, die nodig is, voordat de machine kan gaan rekenen. Volledigheidshalve volgen hier de belangrijkste stadia:
1\(^e\). mathematische formulering van het probleem,
2\(^e\). mathematische oplossing van het probleem,
3\(^e\). keuze of constructie van numerieke processen, die (in het licht van 2\(^e\)) tot het gewenste antwoord leiden,
4\(^e\). programmering: gedetailleerde opbouw van de onder 3\(^e\) genoemde processen uit de elementaire bewerkingen, waartoe de machine direct in staat is,
5\(^e\). codering: uitschrijven van het programma in de code der machine, zodat hierna de band onmiddellijk geponst kan worden.5
Verder zegt Dijkstra:
De idealen, die men bij het maken van een programma nastreeft, zijn de volgende:
1\(^e\). maximale snelheid, vereist om het programma uit te voeren,
2\(^e\). minimale geheugenruimte, vereist om het programma op te bergen,
3\(^e\). maximale veiligheid,
4\(^e\). maximale accuratesse,
5\(^e\). maximale souplesse,
6\(^e\). maximale overzichtelijkheid.6
Omdat bepaalde stukken code regelmatig voor zullen komen, of omdat ze ook in andere programma’s gebruikt kunnen worden is het zinnig subroutines te gaan gebruiken. Zo’n subroutine staat ergens in het geheugen, en bij aanroep wordt in Aa de koppelopdracht of link “meegegeven”, de subroutine plaatst deze koppelopdracht, dat is een sprong terug naar de volgende opdracht na uitvoeren van de subroutine, aan het einde van de subroutine. In S kan bijvoorbeeld een parameter meegegeven worden.
Het rapport wordt besloten met enkele voorbeelden waar het hele programmeerproces in beschreven staat: eerst de mathematische uitwerking, dan het programmeren via bijvoorbeeld een blokschema en uiteindelijk het programma en eventueel het ponsvoorschrift.
Zowel de ARRA II als de beschrijving van de ARRA II zijn beter dan die van de ARRA. Er is duidelijk sprake van een ontwikkeling, men heeft ervaring in het bouwen en gebruiken van automatische rekenmachines gekregen en dat vertaald zich dan ook in ontwerp en documentatie van de nieuwe machine.
Naast deze functionele beschrijving heeft Dijkstra ook het rapport In- en uitvoer van de ARRA7 geschreven in 1954. In het voorwoord schrijft hij dat dit rapport
liggen vastgelegd de programma’s voor het bandlezen en het typen, benevens de hieruit voor[t]vloeiende ponsconventies en aanwijzingen aangaande het gebruik van de typroutines. De hoofdstukken 7 en 8 van het rapport MR 12 [functionele beschrijving van de ARRA] komen hiermede te vervallen.’8
Het in- en uitvoer programma was dus het belangrijke programma en verbetering was blijkbaar mogelijk of noodzakelijk.
In principe kan de in- en uitvoerprogramma’s gezien worden als de software van de ARRA: zo goed als iedereen gebruikte het, zonder deze programma’s zou het gebruik van de ARRA zo goed als onmogelijk zijn. Het is niet vreemd dat hier veel tijd aan besteed werd. Het belang van in- en uitvoer wordt nog maar eens onderstreept als in 1955 wederom een rapport over de in- en uitvoer voor de ARRA wordt uitgebracht.
Het communicatieprogramma van de ARRA9 is geschreven omdat de in- en uitvoerapparatuur van de ARRA werd vernieuwd door uitbreiding van de bandleesopdracht, de versnelling van de kanaalwisseling en de de typmachine. In- en uitvoer was belangrijk in het gebruik van de machine.
Naast in- en uitvoer was er nog een ander algmeen programma dat een eigen rapport verdiende: het rekenen met drijvende komma. In 1954 verschijnt “Drijvende-komma”-rekentechniek (ARRA-subroutines Rd1 en Rd2)10 Rd1 is de subroutine om met drijvende komma te rekenen, Rd2 is de in- en uitvoerroutine voor drijvende komma’s en is pas gedurende het gebruik van Rd1 ontstaan. Verder is het werken met deze subroutine 40 tot 50 maal trager.11 In principe maakt Rd1 van de ARRA een machine met drijvende komma operaties.
De ARRA II was dus duidelijk een machine die beter geschikt was om mee te werken dan de ARRA I, zowel wat betreft hardware als wat betreft de “software”, de in- en uitvoerprogramma’s en de drijvende komma subroutines. Dat uit zich ook in de cursus Programmeren voor automatische rekenmachines12 die in 1955 en 1956 werd gehouden onder leiding van Van Wijngaarden en Dijkstra. In 18 lessen werd het gebruik van computers uitgelegd.
Deze cursus is veel beter te begrijpen dan de eerder besproken technische rapporten: het geeft inzicht in hoe je zo’n computer kunt programmeren en gebruiken en niet alleen informatie over alle mogelijkheden van een specifieke machine. Alhoewel de opzet algemeen van aard was, dus geschikt voor alle computers, wordt waar nodig wel de ARRA II gebruikt als het voorbeeld. Een jaar later, in november 1947, werd de cursus overgedaan maar dan met betrekking op de ARMAC. Deze cursus wordt in de paragraaf over de ARMAC besproken omdat er weinig verschillen zijn, en die van de ARMAC verder uitgekristalliseerd is.
4 FERTA
Nadat de ARRA II gereed was gekomen, werd voor Fokker een vergelijkbare machine gebouwd, de FERTA. Over de FERTA zijn twee rapporten verschenen, beide van de hand van Dijkstra: handboek voor de programmeur FERTA deel I13 en handboek voor de programmeur FERTA deel II14. Het eerste deel handelt over de machine en het programmeren ervan in het algemeen en het tweede gaat over de communicatieprogramma’s.
Vaak wordt gesteld dat de FERTA een tweede ARRA zou zijn, maar ‘verbeteringen, wijzigingen en uitbreidingen zijn echter zo ingrijpend, dat op FERTA niet van toepassing zijn de eerder van de hand van E.W. Dijkstra verschenen rapporten over het programmeren voor de ARRA.’15 Aan de andere kant was deze machine natuurlijk wel gebaseerd op de ARRA, zo was het bedieningspaneel bijvoorbeeld vergelijkbaar. Kijken we naar de opdrachten, dan zien we toch een aantal verschillen.
| 0,n | (A)’ = (A) \(+\) (n) |
| 1,n | (A)’ = (A)\(-\)(n) |
| 2,n | (A)’ = (n) |
| 3,n | (A)’ = \(-\)(n) |
| 4,n | (n)’ = (A), (C)’ = (A)\(_{29}\)’ |
| 5,n | (n)’ = \(-\)(A), (C)’ = 1 \(-\) (A)\(_{29}\)’ |
| 6,n | als (C) = 0, dan (T)’ = n |
| 7,n | (T)’ = n |
| 8,n | (S)’ = (S) \(+\) (n) |
| 9,n | (S)’ = (S)\(-\)(n) |
| 10,n | (S)’ = (n) |
| 11,n | (S)’ = \(-\)(n) |
| 12,n | (n)’ = (S), (C)’ = (S)\(_{29}\)’ |
| 13,n | (n)’ = \(-\)(S), (C)’ = 1 \(-\) (S)\(_{29}\)’ |
| 14,n | als (C) = 0, dan (T)’ = n\(+ \frac{1}{2}\) |
| 15,n | (T)’ = n\(+ \frac{1}{2}\) |
| 16,n | [AS]’= [n].[s] \(+\) [A] |
| 17,n | [AS]’= -[n].[s] \(+\) [A] |
| 18,n | [AS]’= [n].[s] |
| 19,n | [AS]’= -[n].[s] |
| 20,n | [n].[S]‘+[A]’=[AS] |
| 21,n | \(-\)[n].[S]‘+[A]’=[AS] |
| 22,n | als (C) = 0, stop |
| 23,n | als (C) = 1, stop |
De notatie iets anders. De deelopdracht is verdwenen. Ook is er een conditieregister C bijgekomen dat uit een bit bestaat en in principe het tekenbit van A of S voorsteld. De schuifopdrachten 22 en 23 zijn vervangen door conditionele stopopdrachten. Verder zijn de opdrachten 24 tot en met 29 speciale codeopdrachten, dat wil zeggen dat het adresgedeelte van zo’nopdracht een code is die een bepaalde opdracht specificeert. Deze opdrachten bevatten onder andere invoer via handregister en getalschakelaars, koppelopdracht, het optellen van +0 bij A of S, typopdrachten, nultest op A, snel optellen van kleine getallen in A, snel vermenigvuldigen van kleine getallen in A en schuifopdrachten.
In het tweede deel van het handboek FERTA wordt het communicatieprogramma uitgebreid besproken. Naast de invoer die al bij de ARRA beschikbaar was, zoals een handregister en gewone ponsband, is er in de FERTA ook een zogenaamde BIBAND modus, waarbij een deel van het geheugen dat uit de computer is geponst, dus binair, ook weer zo ingelezen kan worden. Dit brengt een snelheidswinst met zich mee: hetinvoerprogramma hoeft niet meer de getallen om te zetten en de instructies op te bouwen uit de gewone ponsinstructies. De uitvoer bestaat uit een typemachine en de eerder besproken biband.
5 ARMAC
Na de ARRA en FERTA werd in 1956 de ARMAC in gebruik genomen. Deze machine zou tot in 1960 gebruikt worden voor het rekenwerk van de Rekenafdeling en externe gebruikers. Over de ARMAC zijn een zestal rapporten in de serie Programmeren voor de ARMAC verschenen, geschreven door verschillende auteurs. Daarnaast zijn er van twee delen een revisie verschenen. Verder zijn er twee “uittreksels” voor intern gebruik geschreven uit het eerste deel van de serie. Of anders gezegd, deze twee “uittreksels” zijn eerder geschreven dan het uiteindelijke document. En als eerder gezegd is de cursus programmeren voor automatische rekenmachines in 1957 nogmaals gehouden, nu met nadruk op de ARMAC.
Omdat de inhoud van de eerste twee “uittreksels” in het daaropvolgende rapport uitgebreid worden behandeld, zal ik hier die twee “uittreksels” niet verder behandelen.
Het eerste deel Programmering voor de ARMAC. Deel I16 is geschreven door Dijkstra. En is vergelijkbaar met de algemene rapporten over de ARRA II en de FERTA. De ARMAC is een uitgebreidere machine, het heeft woorden van lengte 34, nog steeds twee opdrachten per woord. Verder is er een trommelgeheugen van 4096 woorden. Daarbij komt een snel geheugen van (uiteindelijk) 16 kanalen (begint met 1 kanaal) in de vorm van een ringkerngeheugenmatrix. Verder is er een buffer, ook een matrix van ringkernen waarin het kanaal van de trommel dat in gebruik is door de huidige opdracht in gebufferd is. De machine is dus stukken sneller dan de ARRA.
| 0/n | (A)\(+\)(n) \(\Rightarrow\) (A) |
| 1/n | (A)\(-\)(n) \(\Rightarrow\) (A) |
| 2/n | \(+\) (n) \(\Rightarrow\) (A) |
| 3/n | \(-\) (n) \(\Rightarrow\) (A) |
| 4/n | \(+\) (A) \(\Rightarrow\) (n); (n) \(\geq +\) 0? of (A) \(\geq +\) 0? |
| 5/n | \(-\) (A) \(\Rightarrow\) (n); (n) \(\geq +\) 0? of (A) \(\leq -\) 0? |
| 6/n | n \(\Rightarrow\) (T) |
| 7/n | n \(+\) \(\frac{1}{2}\) \(\Rightarrow\) (T) |
| 8/n | (S)\(+\)(n) \(\Rightarrow\) (S) |
| 9/n | (S)\(-\)(n) \(\Rightarrow\) (S) |
| 10/n | \(+\) (n) \(\Rightarrow\) (S) |
| 11/n | \(-\) (n) \(\Rightarrow\) (S) |
| 12/n | \(+\) (S) \(\Rightarrow\) (n); (n) \(\geq +\) 0? of (S) \(\geq +\) 0? |
| 13/n | \(-\) (S) \(\Rightarrow\) (n); (n) \(\geq +\) 0? of (S) \(\leq -\) 0? |
| 14/n | n \(\Rightarrow\) (T) als (C) = 0 en (T) \(+\) \(\frac{1}{2}\) \(\Rightarrow\) (T) als (C) = 1 |
| 15/n | n \(+\) \(\frac{1}{2}\) \(\Rightarrow\) (T) als (C) = 0 en (T) \(+\) \(\frac{1}{2}\) \(\Rightarrow\) (T) als (C) = 1 |
| 16/n | [A] \(+\) [n].[s] \(\Rightarrow\) [AS] |
| 17/n | [A] \(-\) [n].[s] \(\Rightarrow\) [AS] |
| 18/n | \(+\) [n].[s] \(\Rightarrow\) [AS] |
| 19/n | \(-\) [n].[s] \(\Rightarrow\) [AS] |
| 20/n | transporteer track van langzaam geheugen naar snel. |
| 21/n | transporteer track van snel geheugen naar langzaam. |
| 22/n | plaats link in A en spring naar de a-opdracht van adres n |
| 23/n | plaats link in A en spring naar de b-opdracht van adres n |
| 24/\(\cdots\) | Schuif- en communicatieopdrachten |
| 25/\(\cdots\) | ” ” |
| 26/\(\cdots\) | ” ” |
| 27/\(\cdots\) | ” ” |
| 28/\(\cdots\) | ” ” |
| 29/\(\cdots\) | ” ” |
De opdrachtenlijst lijkt meer op die van de FERTA dan op die van de ARRA, de FERTA is duidelijk een stap in de ontwikkeling van de ARMAC geweest en niet zomaar een kopie van de ARRA. Er zijn een aantal opdrachten bijgekomen door de introductie van het snelle geheugen. De basis, de operaties op A en S en de subroutineopdrachten, is hetzelfde gebleven.
De schuif- en communicatieopdrachten bevatten nultesten, handregisteropdrachten, getalschakelaaropdrachten, bandlees en ponsopdrachten, type en terugleesopdrachten, conditionele stopopdrachten, de bufferschrijfopdrachten, de adresloze optelling en de schuifopdrachten. Opvallend bij de typeopdrachten is de toevoeging van het typen van letters: dit is een duidelijke verbetering met de voorgaande typemachines.
in de ARMAC zijn een aantal standaardsubroutines permanent aanwezig in het geheugen: worteltrekken, sinus en cosinus, exacte deling en breukendeling. Er is ook een biband optie aanwezig zoals bij de FERTA. De totale in- en uitvoermogelijkheden en programmatuur zijn sterk verbeterd en vergroot. Er is bijvoorbeeld een layoutprogramma toegevoegd om getallen netjes op een pagina te kunnen afdrukken.
De ARMAC is weer een stukje complexer en beter toegerust voor zijn taak dan zijn voorgangers. Naast deze standaardmogelijkheden zijn er ook een aantal extra mogelijkheden toegevoegd door middel van programma’s. Deze worden besproken in de delen 3 tot en met 6 van de serie. In deel 2 van de serie staat de inhoud van de geblokkeerde kanalen (17 stuks) in het geheugen uitgeschreven, dat zijn dus de programma’s, codes en informatie die standaard in de machine zitten.
Deel drie (Dijkstra) gaat over het rekenen met drijvende komma’s plus een aantal hulpsubroutines zoals de arctangens, de 2-macht en de 2-logaritme. Rd1 simuleert als het ware een een-adres machine met een register R in het rekenorgaan en een aantal opdrachten die uitgevoerd kunnen worden met getallen van drijvende komma, een aantal extra standaard functies, een typinstructie, maar ook met eigen sprongoperaties. In een later toevoeging in 1957 werd ook nog een interpretatief programma voor complexe getallen met drijvende komma’s toegevoegd en het geheel verbeterd. Dat deel is door N.C. Bakker geschreven.
Deel vier, geschreven door L. Vasmel-Kaarsemaker, is een interpretatief programma om met 6-voudige lange getallen te kunnen werken, dus getallen die 6 woorden beslaan, dus getallen tussen \(10^{18}-1\) en \(1.10^{-36}\). Ook hier wordt een nieuwe machine gesimuleerd met een register R, invoer en uitvoer, sprongen, en standaardfuncties.
In deel vijf, door Dijkstra, wordt een interpretatief programma beschreven voor breuken van dubbele lengte en een aantal subroutines zoals reciproke faculteit, derdemachtswortel en teksttypen.
Deel zes , door T.J. Dekker, betreft het Matrix-complex RAM: een complex van matrixprogramma’s voor het eenvoudig werken met matrices.
Zoals eerder gezegd is er naast deze technische rapporten ook een cursus. Die cursus is interessant omdat daarin verteld wordt hoe men zou moeten programmeren. De cursus werd voor het eerst gehouden in 1955 en 1956 in 18 delen onder leiding van Van Wijngaarden en Dijkstra. Meer dan een jaar later, in november 1957 werd de cursus herhaald.
Het doel van de cursus was niet zozeer om te leren werken met de ARRA of de ARMAC, maar om, en de titel verwijst er ook naar, te leren werken met een automatische rekenmachine in het algemeen. Dat neemt niet weg dat het werken met een computer in deze tijd betekende dat men voldoende kennis over de machine waar mee men werkte moest hebben om het berhaupt te kunnen programmeren. Hierdoor wordt in de eerste cursus, waar nodig, ingegaan op de ARRA en in de tweede cursus op de ARMAC.
De cursus begint met een algemene inleiding over automatische rekenmachines waarin een kenschets wordt gegeven van automatische rekenmachines:
tegenwoordig kan men amper spreken van “werk uit handen nemen”: de problemen, waarbij de machtigste der moderne machines pas goed tot hun recht komen, zijn dusdanig omvangrijk, dat men er zonder deze rekenapparatuur nooit aan zou zijn begonnen! Er worden problemen mee aangepakt, die vroeger de meest drieste niet eens als “numeriek probleem” zou durven te beschouwen; en inderdaad, naarmate de methoden, waarop de machines hun resultaten afleveren, geraffineerder worden, raakt het numeriek karakter althans voor de naïeve bezoeker, ernstig op de achtergrond.17
Hierna komen de typische onderdelen van zo’n automatische rekenmachine aan bod: besturing, geheugen, invoer, uitvoer en rekenorgaan.
Het tweede onderwerp van de cursus is het woord waarin uitgelegd wordt dat een woord bestaat uit binaire cijfers die op verschillende manieren geïnterpreteerd kunnen worden: als getal, als opdracht, of als een code. De lengte van een woord hangt samen met de grootte van het geheugen en de gewenste precisie van getallen: in een opdracht kan het functiegedeelte vrij klein zijn omdat een machine over het algemeen maar weinig functies kent. Het numerieke gedeelte van de opdracht is een adres, en alle adressen van het geheugen moeten op deze manier bereikt kunnen worden. In de ARMAC worden 5 bits gebruikt voor het functiegedeelte en is het geheugen met 12 cijfers volledig te benaderen. Dit zou betekenen dat een woordlengte van 17 cijfers voldoende zou zijn, maar men wil getallen met een hogere precisie kunnen weergeven. Daarom is het woord van de ARMAC 34 bits lang, en zitten er twee opdrachten in een woord.
Het getal is het derde onderwerp. Er wordt uitgelegd hoe een geheel getal en een breuk gerepresenteerd worden in een woord. Dat getallen volgens het zogenaamde inversensysteem worden beschreven. Het hoofdstuk wordt afgesloten met de introductie van een aantal schrijfwijzen voor de interpretatie van een woord: (x) is de inhoud van adres x, [x] is dezelfde inhoud van het adres geïnterpreteerd als een geheel getal, {x} geïnterpreteerd als een breuk, [x,y] is een geheel getal van dubbele lengte, [x,y} is [x] + {y} en {x,y} = {x} + {y}.\(2^{-n+1}\).
Hierna is de opdracht aan de beurt. Omdat opdrachten te sterk verbonden zijn met de machine waarop ze werken, wordt in dit hoofdstuk de opdrachten van de ARMAC (en eerder ARRA) besproken. Wel wordt de opmerking gemaakt dat ‘het uit ervaring is gebleken, dat iemand, eenmaal met de “opdrachtencode” van een bepaalde machine vertrouwd, snel die van een andere machine leert en vooral beter de merites ervan begrijpt.’18 Dit hoofdstuk beslaat enkel een zestal kleine voorbeelden en wat opgaven, voor meer informatie wordt naar MR 25 verwezen, waarin de ARMAC en haar code wordt beschreven. In de eerdere cursus wordt wel de opdrachtencode van de ARRA gegeven, maar niet verder uitgediept.
Dan komt een interessant hoofdstuk over het proces van programmeren en met name over het maken van blokschema’s oftewel flow diagrams. De noodzaak of zin van blokschema’s wordt uitgelegd:
Voor de geïnteresseerde, die het programma inkijkt, zelfs voor de programmeur, die het programma opgesteld heeft, houdt deze “verstaanbaarheid” echter niet over: het lezen van een programma van de opdrachten alleen, zonder een blik te slaan op in de explicatie, die er gelukkig doorgaans we naast staat, vergt erkend veel geduld en doorzettingsvermogen. Dit is wel te verklaren.
Een van de redenen, dat men gauw in de veelheid van opdrachten omkomt, is zeker, dat er dikwijls veel opdrachten nodig zijn, om te berekenen, wat de lezer als één logisch geheel beschouwt (b.v. \(x^5\) of \(sinx\)). Een tweede oorzaak, waardoor de structuur van het programma neigt schuil te gaan, is daarin gelegen, dat het programma belast is met veel irrelevante informatie: de plaats, waar alle opdrachten en getallen staan, ligt in een feitelijk programma vast, terwijl voor dezelfde gang van de berekening het geheugen best anders ingedeeld had kunnen zijn en alles net zo goed op andere adressen had kunnen staan. Het belangrijkste is echter wel, dat in het programma wel staat, wat er gebeurt, maar niet, wat dit nu allemaal behelst: er staat, onder welke omstandigheden een conditionele besturingsverplaatsing gehoorzaamd wordt, wat echter in de zin van deze speciale omstandigheden is, wordt aan de intelligente lezer overgelaten ….. Kortom er is een behoefte aan overzichtelijke weergave van programma’s, een notatie waarin, dank zij verzwijging van de bijkomstigheden de essentialia niet verdrinken en waar tevens de functie van de stukken programma (en van de “voorzorgen”) in aangegeven is.19
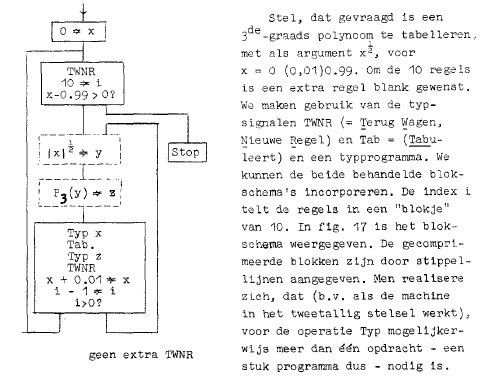
Bijkomend voordeel van blokschema’s is dat het een machine onafhankelijke notatie is, dus uitermate geschikt voor deze cursus. Nadeel van blokschema’s is deze minder efficiënt zijn dan ‘uitgekookte “getructe” programma’s’20. Dergelijke programma’s zijn toch nodig, denk aan standaardprogramma’s waar alles uit de machine gehaald wordt, waar ‘geraffineerd van de - vaak onbedoelde! - speciale eigenschappen van de machine’21 wordt gebruik gemaakt.
In een blokschema worden opdrachten in blokken opgedeeld die met lijnen verbonden zijn. De conventie is dat een blok altijd van boven binnengekomen wordt en onder verlaten. Verder, in geval van een keuzemogelijkheid, dan staat er boven een vraag, is de rechteruitgang de ja en de linker de nee. Verder wordt een notatie gebruikt die ontleend is aan Rutishauser: het gerichte gelijkteken een soort is-teken met een groter dan teken erdoor. Dus de linkerkant van dit teken wordt toegekend aan de rechterkant van dit symbool. Voor een mooi voorbeeld van een programma in blokschemavorm:
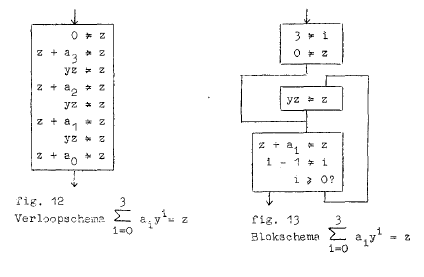
In deze cursus wordt ook een zogenaamd verloopschema geïntroduceerd, dat in de vorige cursus nog niet aanwezig was. In zo’n verloopschema wordt aangegeven hoe, vanboven naar beneden, en in welke vorm de berekening in de tijd verloopt, dus in welke volgorde de aritmetische operaties uitgevoerd worden. Veelal is zo’n verloopschema bedoeld om een hoop vergelijkbare operaties weer te geven, vaak niet zonder de welbekende puntjes om dat aan te geven. Een dergelijk schema kan in eenblokschema omgezet worden door de introductie van een teller en een iteratie. Zo’n programma is vaak langzamer dan het gestrekte programma waar alle operaties uitgeschreven zijn. Maar het gestrekte programma neemt natuurlijk te veel geheugenruimte in beslag en het programma is afhankelijk van het aantal opdrachten. Dus in een verloopschema staat wat een machine moet rekenen en in het blokschema hoe het moet rekenen. Een voorbeeld is gegeven in de afbeelding hierboven.
Nadat blokschema’s geïntroduceerd zijn, verschuift de aandacht naar subroutines. Subroutines zijn enorm tijdbesparing doordat ze hergebruik van programma’s (programmadelen) mogelijk maken. Zo zijn er verschillende wiskundige functies die altijd maar weer gebruikt worden in programma’s en als eenmaal dergelijke functies uitgeprogrammeerd zijn in een subroutine dan kunnen ze herhaaldelijk in een echt programma gebruikt worden.
De subroutine staat op een bepaalde plaats in het geheugen en wordt door het programma aangeroepen door een sprong naar de subroutine. Bij die sprong wordt informatie meegegeven: de parameters en het terugkeeradres waar het programma na uitvoering van de subroutine weer verder gaat. In de ARMAC gaat dit via een zogenaamde koppelopdracht die bij aanroep van een subroutine in het lage deel van het A register geplaatst wordt. Bij het begin van de subroutine wordt deze koppelopdracht aan het einde van de subroutine op een opengelaten adres geschreven. In de ARMAC gebeurt dit door de opdrachten 22 en 23.
Door dergelijke standaard subroutines wordt als het ware de beperkte opdrachtencode van de machine uitgebreid met allerhande bruikbare en veelgebruikte opdrachten. Bij de armac staan veel subroutines op een standaard-band of op een automatisch vervaardige kopie waardoor het ponswerk sterk gereduceerd wordt. In een blokschema worden subroutines aangegeven door een met een stippellijn omgeven blok.
Er worden verschillende soorten subroutines onderscheiden: eenvoudige subroutines waarin geen andere subroutines worden aangeroepen zijn nulde orde subroutines. Een subroutine die een andere subroutine aanroept is van de orde n+1 als n de orde van de aangeroepen subroutine is.
Hierna wordt een groter voorbeeld uitgewerkt in hoofdstuk 7. Bij de vorige cursus werd eerst nog de invoer en uitvoer van de ARRA besproken, maar in deze nieuwe cursus is de invoer en uitvoer besproken tussen de regels door. Het voorbeeld is het oplossen van \(x^2 + y^2 = G\), \(G\) een non-negatief getal en verder geldt: \(x\) en \(y\) zijn gehele getallen en \(x\) en \(y\) voldoen aan \(0\leq x \leq y\). Het gehele programmeerproces wordt doorlopen: eerst de wiskundige onderzoeking van het probleem en de oplossing, daarna het blokschema en uiteindelijk de programmacode.
Dan volgen een aantal uitwerkingen van standaardfuncties in subroutines op verschillende manieren, zoals de wortel, de deling, de sinus en cosinus, de arctangens \(\frac{y}{x}\), de e-macht, logaritme met grondtal 2.
Dan volgt een bespreking van snelheid. Snelheid is voor een groot deel machine afhankelijk, maar een programmeur kan over het algemeen de machine zelf niet aanpassen. De snelheidsbeperkende factor is het geheugen, het ophalen van opdrachten en gegevens uit het geheugen is duur. Gegevens en opdrachten kunnen echter zo geplaatst en gelezen worden dat er een grote snelheidswinst te behalen valt. Bij de ARMAC is een snel geheugen beschikbaar dat als buffer dient: een heel kanaal van het langzame trommelgeheugen wordt in de buffer ingelezen op het moment dat deze nodig zijn. Omdat opdrachten en gegevens vaak bij elkaar staan, betekend dit een enorme snelheidswinst: er hoeft maar een keer per kanaal op de trommel gewacht te worden en niet meer bij elke geheugenactie. Daarnaast is er nog een snel geheugen beschikbaar dat door de programmeur gebruikt mag worden. Bij de ARRA was er geen snel geheugen dus daar had men een andere oplossing.
Door het snelle geheugen in de ARMAC hoeft de programmeur zich eigenlijk geen zorgen meer te maken over een verstandige plaatsing van gegevens op de trommel. Enkel bij programma’s waar veel geheugenoperaties nodig zijn, zoals bij matrixverwerking, is dit weer van belang.
Naast snelheid spelen ook schaling, controle en flexibiliteit een rol. Schaling is het vermenigvuldigen van constanten en variabelen met geschikt gekozen factoren waardoor ze een hanteerbare orde van grootte krijgen. Schaling werkt alleen als men een goed idee heeft van de orde van grootte van variabelen en constanten. Heeft men dat niet, dan moeten andere getalrepresentaties gebruikt worden, bijvoorbeeld die van de drijvende komma.
Controle zijn alle maatregelen die de programmeur treft om er zeker van te zijn dat de resultaten overeenkomen met de bedoelde resultaten. Een manier is om elke berekening twee maal uit te voeren en dan de uitkomsten te vergelijken: zijn ze gelijk dan zal het wel goed zijn, is het ongelijk, dan stopt de machine. Een dergelijke controle is onwenselijk en er zijn vele verschillende controlemechanismen ontwikkeld. Bij de ARMAC is dat eigenlijk niet meer nodig omdat er een paritycheck is ingebouwd. Bij elk half woord schrijven in het geheugen wordt een 18de bit toegevoegd zo dat het aantal enen in het achttiental oneven is. Bij het lezen wordt gecontroleerd of het aantal enen oneven is. Is dat niet het geval, dan stopt de machine. Verder is dit een goede indicatie van de toestand van het geheugen.
In tegenstelling tot het verleden is nu het stadium bereikt, dat de zwakste schakel in het proces niet meer de machine, maar —– de programmeur is! En de programmeur doet er goed aan met behulp van het programma zichzelf te controleren.22
Zo kan een geprogrammeerde controle gebruikt worden om van te voren vast te stellen of alles goed hoort te gaan. Verder helpt het bij ons gebrek aan accuratesse, bijvoorbeeld bij het ponsen.
Flexibiliteit betekend in de eerste plaats herstartbaarheid wanneer een programma is gestopt bij een machinefout of bij het testen. Maar ook het eenvoudig kunnen aanbrengen van wijzigingen in een programma behoort tot flexibiliteit. Of sterker nog, bij meer algemene programma’s, zodra een programma (her)gebruikt kan worden door een ander moet de flexibiliteit nauw in het oog gehouden worden.
Kortom: de moeilijkheid is dat veelal de wens naar voren zal komen een bestaand programma te gebruiken op een manier, die niet precies bedoeld was, voor een probleem, waarvoor het programme niet precies gemaakt was. De programmeur maakt het programma, d.w.z. een precieze formulering van het rekenschema: aan hem wordt overgelaten, rekening te houden met allerlei mogelijke nog niet geformuleerde eisen.23
De volgende onderwerpen van de cursus zijn subroutines en programma’s van een hogere orde: administratieve subroutines en superprogramma’s. Een administratieve subroutine is een subroutine die een coördinerende taak heeft, ze roepen andere subroutines aan. Als voorbeeld wordt gegeven een subroutine die voor x, f(x) en delta f(x) uittyped. Het hoofdprogramma rekent de waarden van f(x) uit, de subroutine maakt het mogelijk om de gegevens netjes uit te typen: dus geen delta f(x) op de eerste regel, het opnieuw typen van een regel bij een nieuwe pagina, het onderdrukken van het typen van f(x) of delta f(x) waar dan wel een juiste tabulatie wordt ingevoegd, etc. Deze subroutine heeft dus verschillende aanroepen om het gewenste resultaat te bereiken. Andere voorbeelden zijn integratie of tabellatie.
Superprogramma’s zijn programma’s die de taak hebben andere programma’s te onderzoeken of te interpreteren of anderszins op programma’s werken. Bijvoorbeeld het uittypen of uitponsen van een gedeelte van het geheugen waardoor een nette kopie van het programma gemaakt wordt. Een ander voorbeeld is het invoerprogramma, dat vertaald programmeurscode naar machinecode. Het idee van deze programma’s is om het leven van de programmeur gemakkelijker te maken. Dit kan door uitbreidingen zoals het drijvend programmaeren24, het ladderen en utility-programma’s.
Voordelen van het drijvend programmeren is de kortheid en flexibiliteit van programma’s. Nadeel is dat optimum programmeren niet meer mogelijk is en dat men niet meer weet waar precies in het geheugen het programma precies staat. Dat laatste probleem is oplosbaar door bij het invoerprogramma gegevens van het programma af te drukken.
Een andere mogelijkheid is het ladderen, het uitschrijven van een programma in plaats van gebruik te maken van lussen (iteraties). Een ladderprogramma kan dat automatisch doen, dit bespaart pons- en invoertijd. Daarnaast zijn er speciale utility-programma’s mogelijk waardoor bijvoorbeeld het invoeren van grote hoeveelheden getallen versneld kan worden door een andere ponsconventie in te voeren voor de gelegenheid.
Deze superprogramma’s behandelen het objectprogramma zoals het is, maar begrijpen niet dat het een levend karakter heeft, dat opdrachten een operationele betekenis hebben.
De vraag rijst - en wordt bevestigend beantwoord - of er superprogramma’s kunnen worden ontwikkeld, die het objectprogramma wezenlijk kunnen interpreteren, d.w.z. met inachtneming van de werking van het objectprogramma. Zulke superprogramma’s heteninterpreterende programma’s. Het objectprogramma kan in de machinecode in de machine aanwezig zijn. In dat geval zou het dus zonder m eer aan het werk gezet kunnen worden. Het nut van het interpreterende programma zou dus dubieus kunnen lijken en ook inderdaad zijn, als het zich alleen beperkte tot het nabootsen van wat het objectprogramma zou doen, als het aan bod was. Het interpreterende programma kan echter behalve dit meer doen, b.v. uittypen welke opdrachten van het objectprogramma gehoorzaamd worden, en voorts welke getallen gemanipuleerd worden, wat de gewijzigde inhouden van de registers van het rekenorgaan zijn, wat de conditie is, enz. Een dergelijk programma is een prachtig hulpmiddel om fouten in een gemaakt programma op te sporen. Het is noodzakelijkerwijs langzaam, zelfs zeer langzaam, maar kan op allerlei wijzen geweldig worden versneld. Het zou nl. ook alle gebruikte subroutines gaan interpreteren, wat kennelijk niet de bedoeling is, (ook de werking van een semi-interpreterende subroutine, terwijl men daar met veel minder informatie zou kunnen volstaan). Door b.v. van te voren te vertellen aan het interpreterende programma, in welk gedeelten van het geheugen het werkelijk te interpreteren objectprogramma staat, kan het volstaan met het interpreteren van dat gedeelte, terwijl het de subroutines vrij laat lopen (bij de koppelopdracht pikt het dan de draad weer op).
(…)
Het samenstel, machines plus interpreterend programma, van deze soort is dan in wezen te beschouwen als een nieuwe machine, een pseudo-machine, die handelt als de echte machine, maar daarnij [daarbij] nog voortdurend verslag uitbrengt van zijn handelingen als een neurotische patiënt aan de psychiater(nl. de programmeur).
Dat een dergelijk programma te maken is, zal wel zonder meer duidelijk zijn op grond van wat tot nu toe behandeld is. Het interpreterende programma moet zelf een pseudo-machine bijhouden in de vorm van een aantal adressen gebruikt als pseudo-opdrachtteller, pseudo-rekenregisters, pseudo-condities, enz. Er rijzen geen principiële moeilijkheden.
Naar aanleiding van de analogie patiënt-psychiater merken wij nog op, dat wij ook het objectprogramma alleen als patiënt kunnen zien. Het interpreterende programma is dan psychiater en het uitgetypte diens aantekeningen. Een hoogst vermakelijk experiment, dat wij jaren geleden op de ARRA pleegden, is het interpreterende programma in duplo in de machine brengen, daarbij elk specimen als objectprogramma aan het andere aanwijzend. Laat men dan één van beide werken , dan verkrijgt men uitgetypt een verslag van psychiater A, die psychiater B’s handelingen analyseert, als deze (B) bezig is A’s handelingen te onderzoeken. Het bleek daarbij, dat het interpreteren van dit verslag de programmeur ook spoedig rijp maakt voor de psychiater.
Een tweede soort interpreterend programma, dat veel nuttiger is, werkt op een objectprogramma, dat in de machine aanwezig is, maar in een andere code dan de machinecode is gesteld. Het samenstel machine plus interpreterend programma van deze soort is te beschouwen als een pseudo-machine van een geheel ander soort dan de oorspronkelijke, b.v. een machine die zonder meer met complexe getallen kan werken of met drijvende komma. Het stelt ons allereerst in staat om een programma met complexe getallen net zo eenvoudig te programmeren als een gewoon programma.
Daarbij dient te worden bedacht, dat zelfs in een programma, dat veelvuldig werkt met drijvende complexe getallen toch nog een aanzienlijk gedeelte, nl. de gehele administratie gewoon kan geschieden. Het is een groot tijdverlies ook de administratie te laten interpreteren. Daarom is het van belang dat men gemakkelijk om kan schakelen tussen interpreteren en niet-interpreteren.
(…)
Een aardige toepassing van dit soort interpreterende programma’s rijst bij het ontwerpen van een nieuwe machine als men zelf beschikt over een andere machine, die in een andere code werkt. Men kan deze nieuwe machine nabootsen door een interpreterend programma op de bestaande machine en daarmede dan de ontworpen programma’s en subroutines voor de nieuwe machine vast controleren.’25
Een derde soort interpreterende programma’s werken op programma’s die zich niet in de machine bevinden maar bijvoorbeeld op band staan. Aan de ene kant zijn er programma’s die de band lezen en daar een machineprogramma van maken (bijvoorbeeld het invoerprogramma, maar meer algemeen formulevertalers, compilers?) en aan de andere kant zijn er zogenaamde compilerende programma’s die direct van de band instructies interpreteren en deze uitvoeren.
Literatuur
-
A. van Wijngaarden, Programmeren voor de ARRA (Amsterdam: Mathematisch Centrum, 1951), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9282A.pdf.↩︎
-
Ibid., 1.↩︎
-
In de jaarverslagen worden ongeveer 33 opdrachten genoemd waarbij het gebruik van de ARRA II expliciet vermeld wordt. Daarnaast waren er ook wat vermeldingen van voorbereiding of intentie tot gebruik van de ARRA, maar is om verschillende redenen niet doorgegaan.↩︎
-
E. W. Dijkstra, Functionele beschrijving van de ARRA (Amsterdam: Mathematisch Centrum, 1953), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9277A.pdf.↩︎
-
Ibid., 33.↩︎
-
Dijkstra, Functionele beschrijving van de ARRA.↩︎
-
E. W. Dijkstra, ‘Drijvende komma’ rekentechniek (ARRA subroutines RD1 en RD2) (Amsterdam: Mathematisch Centrum, 1954), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9273A.pdf.↩︎
-
Ibid., voorwoord.↩︎
-
E. W. Dijkstra, Het communicatieprogramma van de ARRA (Amsterdam: Mathematisch Centrum, 1955), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9268A.pdf.↩︎
-
E. W. Dijkstra, In- en uitvoer van de ARRA (Amsterdam: Mathematisch Centrum, 1954), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9275A.pdf.↩︎
-
Ibid., voorwoord. Trager dan wat is de vraag, waarschijnlijk trager dan de drijvende komma zelf uitprogrammeren in een programma. Het kan ook betekenen trager dan met vaste komma rekenen.↩︎
-
E. W. Dijkstra, Het standaard typprogramma van ARMAC (Amsterdam: Mathematisch Centrum, 1956), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9265A.pdf.↩︎
-
E. W. Dijkstra, Handboek voor de programmeur (FERTA) I (Amsterdam: Mathematisch Centrum, 1955), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9272A.pdf.↩︎
-
E. W. Dijkstra, Handboek voor de programmeur (FERTA) II (Amsterdam: Mathematisch Centrum, 1955), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9269A.pdf.↩︎
-
Dijkstra, Handboek voor de programmeur (FERTA) I, 1.↩︎
-
E. W. Dijkstra, Korte beschrijving van de opdrachtencode etc. voor de ARMAC (Amsterdam: Mathematisch Centrum, 1956), http://repos.project.cwi.nl:8888/cwi_repository/docs/I/09/9266A.pdf.↩︎
-
T. J. Dekker, E. W. Dijkstra, en A. van Wijngaarden, Cursus programmeren voor automatische rekenmachines (Amsterdam: Mathematisch Centrum, 1957), 1, http://www.cs.utexas.edu/users/EWD/MCReps/CR1957-009.PDF.↩︎
-
Ibid., 18.↩︎
-
Ibid., 20.↩︎
-
Ibid., 21.↩︎
-
Ibid.↩︎
-
Ibid., 79.↩︎
-
Ibid., 82.↩︎
-
Er wordt verwezen naar M.V. Wilkes, ‘The use of a “floating address” system for orders in an automatic computer’, Proc. Cambridge Phil. Soc. 49 (1953, part 1, 84)↩︎
-
Dekker, Dijkstra, en Wijngaarden, Cursus programmeren voor automatische rekenmachines, 103–5.↩︎
