This chapter is based on Huub de Beer, Koeno Gravemeijer, & Michiel van Eijck (2018) ‘Exploring Instantaneous Speed in Fifth Grade’ Educational Designer Vol. 3, No. 10 http://www.educationaldesigner.org/ed/volume3/issue10/article39/.

1 Introduction

Design research emerged in the 1990s as a reaction to a perceived gap between educational practice and research (Eerde, 2013; Reeves, McKenney, & Herrington, 2010; The Design-Based Research Collective, 2003). To bridge that gap, design research builds on educational design to take real-world educational practice into account while using a process of iterative refinement to create both a product and a theory that explains how that product works in terms of students’ learning processes (Barab & Squire, 2004; Cobb, 2003; Plomp, 2013). However, most products of design research do not evolve beyond mere prototypes (Burkhardt & Schoenfeld, 2003; Schoenfeld, 2009), which could potentially limit the utility of the accompanying theory. From an educational design perspective, Schoenfeld (2009) attributes this problem to the fact that many design researchers do not seem to understand the need for both theoretical development and practical design. As a solution, he proposed that design research is to be carried out in balanced project teams (Schoenfeld, 2009). However, this might not be a realistic option for many a design research project. Since design research is ultimately used in research settings, the proportion of research expertise in project teams often exceeds that of educational design expertise. It would further suggest researchers have to acquire the necessarily educational design skills somehow.

Unfortunately, one can only learn to become an educational designer through an inefficient process of experimentation and apprenticeship because educational design lacks both an institutionalized form of schooling and professional literature (Schunn, 2008). To professionalize educational design practice, Schunn (2008) suggests to model it after the field of engineering, which has a long standing tradition of scholarship and education on design practices. Schoenfeld (2009) continues this argument and proposes that the educational design community starts documenting their practices and knowledge. We concur, and we see a role for design research in this regard. Design research may take various forms, the type of design research we have in mind here focuses on learning processes (Gravemeijer & Cobb, 2013). In this type of design research, special attention is paid to the origin and development of the theoretical claims, in a process, which to a large extent comes down to documenting both the actual educational-design practice and the knowledge construction. In this sense, design research may offer indications for a similar approach in educational design.

Design research does not follow a (quasi-)experimental research design. Instead, the process by which claims are produced will have to justify its results in a more direct manner. In relation to this, Smaling (1990) borrows “virtual repeatability” from ethnography as an alternative for the prevailing criterion of repeatability. He links this methodological norm of virtual repeatability to the criterion of “trackability”. Outsiders should be able to retrace the learning process of the researchers in such a manner that it becomes virtually repeatable for them. This then would allow them to judge the credibility of the claims themselves.

Characteristics for design research with a focus on learning processes is that the design revolves around the mental activities of the students. Here we may think of Simon’s (1995) notion of a hypothetical learning trajectory, which describes the anticipated mental activities the students will engage in when they participate in the envisioned instructional activities, and how those mental activities relate to the learning goals. It is the design, trial, evaluation, and revision of a series of such hypothetical learning trajectories that is at the heart of the learning process of the designers. The consecutive hypothetical learning trajectories are reflexively related to the so-called local instruction theory. The local instruction theory constitutes the rationale for the instructional sequence that is being developed and consists of a theory about a possible learning process for a given topic, and the means of supporting that process. That is, the researchers start out with a conjectured LIT, which is revised and adapted during multiple design experiments.

In this paper we describe such a learning process to illuminate how design research may contribute to the codification of educational design practices. While at the same time trying to show that design research can produce theory that is relevant for educational designers.

In the design research project we discuss here, we followed the approach outlined in Gravemeijer & Cobb (2013) in order to develop a local instruction theory (LIT) on teaching instantaneous speed in 5th grade. This LIT, and the prototypical instructional sequence by which it was instantiated, was elaborated, adapted, and refined in three macro design-cycles called design experiments (Cobb, 2003; Gravemeijer & Cobb, 2013) (Figure 1). A design experiment has three phases. In the preparatory phase, the LIT is (re)formulated and used to design an instructional sequence. Subsequently, that instructional sequence is tried in a teaching experiment that consists of a sequence of micro design-cycles of (re)developing, trying out, evaluating, and adapting instructional activities and materials (Figure 1, blue cycles). Next, a retrospective analysis is carried out. This analysis of what happened during the teaching experiment informs a second round of analysis of how the design affected students’ learning processes. The results are used to refine the LIT, which acts as the starting point of the next design experiment. Before the first design experiment is conducted, design research is started up by elaborating the potential learning goals, and exploring the literature and any other sources that might contribute to the researchers’ understanding of students’ prior conceptions.

In the next section, we explore the development of the instructional sequence and the corresponding LIT and its justification by describing our own learning process during the development of an instructional sequence on instantaneous speed in our design research. Next, we elaborate this justification further by detailing its role in pertaining to the trackability of our research. Finally, we discuss these justifications in light of the relationship between educational design and design research.

2 Interwoven development of the LIT and our own learning process

In this section we describe the development of the LIT to illuminate our own learning process during the development of an instructional sequence on instantaneous speed in our design research project. As it is nigh impossible to give a full and complete account of our learning process, we focus on the main learning moments and we will briefly summarize what we learned after each design experiment.

2.1 Forming our initial ideas

This section is summary of the results and findings presented earlier in H. de Beer, Gravemeijer, & Eijck (in preparation).

2.1.1 Starting up

We started by reviewing the literature on primary-school students’ conceptions of speed. We found that both in this literature and in the primary curriculum speed is mostly limited to average speed in the context of motion and described by a ratio; instantaneous speed is not mentioned. Instantaneous speed is conventionally first taught in a calculus course, we therefore widened our review to the literature on teaching calculus-like topics earlier in the mathematics curriculum than calculus is conventionally taught. Most of these initiatives used computer simulations and graphs: it enables students without much algebraic skills to reason about change (Kaput & Schorr, 2007; Stroup, 2002). Exemplary is Stroup’s (2002) “qualitative calculus” approach to teaching calculus-like topics. Stroup critiques the conventional instruction of rate, which treats intuitive qualitative understanding of rate merely as a transitional phase towards a ratio-based understanding of rate, and he argues developing a qualitative understanding of rate is a worthwhile enterprise in and of itself. We decided to aim at expanding on this approach by supporting 5th graders in developing both a qualitative and a quantitative understanding of rate.

In our search to develop a conception of instantaneous speed while circumventing the complex process of taking the limit of average speeds we looked at the historical development of the concept of instantaneous speed. Long before a formal mathematical definition, an intuitive notion already existed (Doorman, 2005): around 1335, William Heytesbury defined his intuitive notion of instantaneous velocity as:

‘a nonuniform or instantaneous velocity (…) is not measured by the distance traversed, but by the distance which would be traversed by such a point, if it were moved uniformly over such or such a period of time at that degree of velocity with which it is moved in that assigned instant.’ (From: Heytesbury (1335) Regule solvendi sophismata, as cited in (Clagett, 1959, pp. 235–237)).

We assumed that the students’ intuitive notions are close to this historical notion. We therefore formulated a LIT on teaching instantaneous speed in 5th grade, in which we aimed at helping the students to explicate and expand these notions.

We chose the context of filling glassware over the motion context, as we feared that the latter might bring with it unreflected terms and procedures. The origin of this context can be traced back to the experienced educational designer Malcolm Swan, who used it in a secondary textbook on functions and graphs (Swan, 1985). We conjectured that the students would come to realize that the speed with which the water level rises in a cocktail glass changes at every instant, and that this speed is continuously diminishing. Building on this insight, the students would come to understand how the shape of a “height-over-time” graph relates to the rising speed in the glass. By discussing the curved shape of this graph we expected that the students could be made aware that the speed changes at every instant. By making the latter a topic of discussion, we would have a starting point for deepening their understanding of instantaneous speed.

2.1.2 Preliminary one-on-one teaching experiments

Before elaborating those ideas further, we carried out a series of one-on-one teaching experiments with nine 5th graders—which we reported on in detail elsewhere (H. de Beer et al., in preparation). We developed a short instructional sequence with the same activities with a highball glass (a cylindrical glass), a cocktail glass, and an Erlenmeyer flask in a (computer simulation). For each glass, the students were asked to:

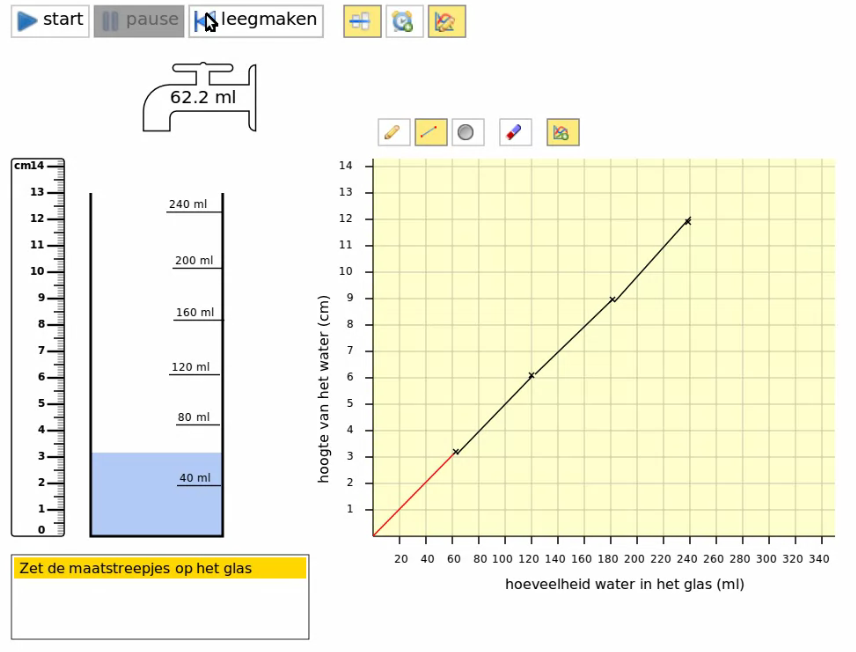
• turn the glass into a measuring cup by dragging hash marks to the right place on the glass (see Figure 2 and 3, left hand side),
• evaluate their solution using the computer simulation,
• draw a graph of filling that glass, and
• again, evaluate their solution using the simulation (see Figure 2 and 3, right hand side).

We performed 8 one-on-one teaching experiments with above average performing 5th graders (in one experiment a pair of students participated).

In the one-on-one experiments, it showed that the students found the linearity of the process of filling a highball glass self-evident, and spontaneously described this process with a linear graph (Figure 2). When carrying out those tasks for a cocktail glass, however, many students initially fell for the so-called linearity illusion (Bock, Dooren, Janssens, & Verschaffel, 2002). Most students made a linear-gauged measuring cup of the cocktail glass. But when they saw a cocktail glass fill up, they quickly realized that the process was not linear. They could relate the decreasing speed to the glass’ increasing width, arguing that the speed decreases because of the growing width of the glass. In line with this realization, the students accepted the computer-drawn curve as a better graph for describing filling the cocktail glass than their own hand-drawn straight-lined graphs. They could not, however, explain the curve. Nor could they come up with such a curve by themselves.

We may briefly summarize what we learned:

• Conceiving filling a (cylindrical) highball glass as a linear process appeared self-evident for the students.
• This was also the case for the linearity of the graph.
• With the cocktail glass they initially fell for the linearity illusion, but when they saw the simulation, they realized that the rising water level slows down.
• They could not draw the correct graph.
• They seemed to appreciate the curve, but could not explain it.

2.2 Design experiment 1

In the first lesson of the teaching experiments of design experiment 1 we tried to imitate the starting-up phase, by asking the students to make measuring cups from the highball glass, the cocktail glass, and the Erlenmeyer flask, and evaluate their work by filling up the glasses in the (computer simulation).

Based on the one-on-one teaching experiments, we expected the students to have no trouble with the highball glass and apply the same linear prototype to the cocktail glass. Once they would observe it fill up, they could realize it is a non-linear situation. The students would relate the decreasing speed to the glass’ increasing width, while formulating the relationship between a glass’ width and speed. Hereafter, the students would be able to coordinate water height and volume.

Next, the students would be asked when the water rises with the same speed in both the highball and cocktail glass. Given their informal understanding of the relationship between a glass’ width and speed, they would be expected to come up with the point where both glasses have the same width. We then wanted to support them in realizing they can compute the speed at a specific point by computing the corresponding virtual highball glass’ speed. When prompted to think of a way to determine the speed at another point, we expected the students to imagine a highball glass with the same width as the cocktail glass at that point, and compute its speed (see Figure 4). After introducing a computer-tool to draw an imaginary highball glass on top of other glasses, the students would have a tool available for measuring instantaneous speed in various glassware.

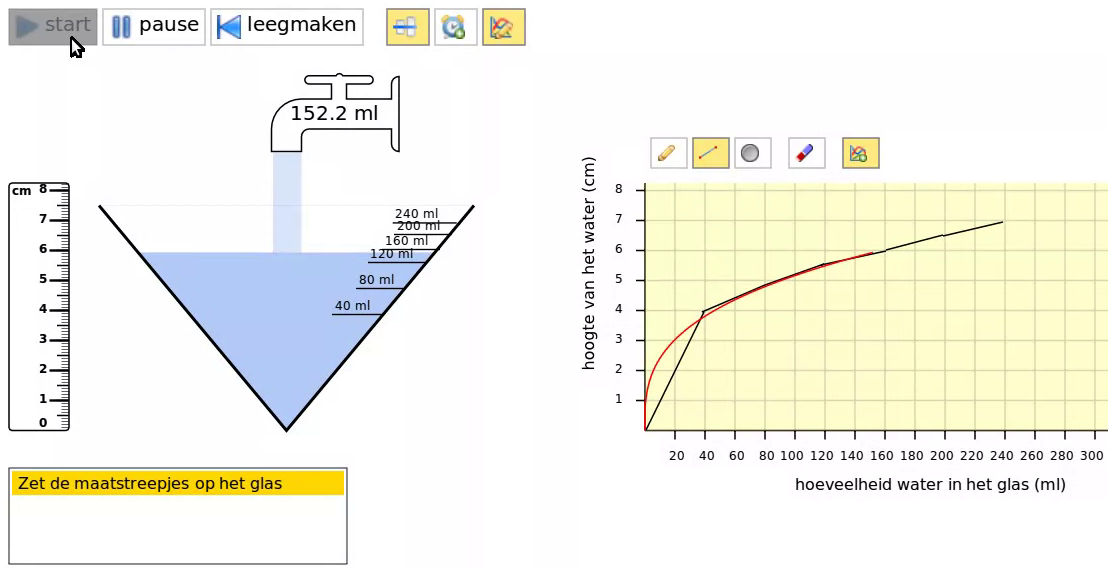
Then, the students would start exploring the changing speed quantitatively by measuring instantaneous speed at various points. We initially planned to deepen their emerging quantitative understanding by having them draw speed-volume graphs. Followed by tasks to reconstruct the shape of a glass on the basis of a glass’ speed-volume graph. However, when trying out this learning trajectory in a mixed 5th-6th grade gifted classroom with an experienced teacher, we observed in the third lesson that the students seemed to become bored with filling glasses. As we had planned one-on-one teaching experiments in between lessons four and five to explore students’ conceptions of speed in other contexts, we decided to alter the fourth lesson by including these activities about other contexts: toy-car racing and daily temperature (see the last four activities of lesson 4).

We realized, however, that to determine speeds in those contexts the students had to be able to work with the tangent line on a curve. We conjectured that by combining the highball-glass-tool and the tangent-line-tool, the students would come to see that the tangent line in a point of the graph corresponds with the linear graph of the speed in the virtual highball glass (Figure 5). Then we expected the students to be able to use the tangent-line as an indicator of the speed in a point of a graph even when the graph is shown without the realistic simulation.

2.2.1 Observations, reflections, and revisions

The first instructional activities were intended to lead the students to coordinate two quantities, but, as a side effect, it made the students think about change in terms of hash marks, height differences, and intervals. This discrete approach to change was being reinforced by the way the teacher approached whole-class discussions about computing speed in the highball glass: she wanted the students to mark measurements from a table as points of the graph first, and then connect the points with straight lines even when some students argued to draw a straight line immediately. She led the class to focus on determining speed on small intervals, without discussing what a computed speed actually meant. Thus, when the highball glass was replaced by the cocktail glass, the students interpreted this non-linear situation in terms of a series of discrete changes. They did have trouble matching that perspective with the continuous changing speed in the cocktail glass.

It showed, however, that the students had no problem whatsoever with the question when the speeds in the cocktail glass and highball glass are the same. Indeed, already at the end of the first lesson the students realized that this would be when the widths were the same. As anticipated, this allowed the students to invent the virtual highball glass as a measure for instantaneous speed. Linking the highball-glass-tool directly with the tangent-line-tool in the computer simulation (see Figure 5), seemed to enable the students to determine instantaneous speeds in the cocktail glass by using the tangent-line-tool, although the extent of their understanding of the tangent line and its relation with speed remained unclear.

In the context of toy-car racing, the students were able to interpret the graph, and most could compute the instantaneous speed using the tangent-line-tool. However, the concept of instantaneous speed was not discussed. And we suspect that the students’ skill in using these tools to compute instantaneous speed was mostly procedural in nature, and not an expression of a deeper understanding of instantaneous speed.

2.2.1.1 Chunky thinking

During the first three lessons, the students displayed what (Castillo-Garsow, Johnson, & Moore, n.d.) denotes a chunky way of thinking, which was also promoted by both instructional sequence and teacher. Castillo-Garsow (2012) introduced the concepts “chunky” and “smooth” to characterize two different forms of reasoning. Thinking about change in terms of intervals, or completed chunks, is called “chunky”. Students with a chunky image of change see change on an interval as the end-result of change on that interval. Students that see change as a continuous process, however, have a “smooth” image of change (Castillo-Garsow, 2012; Castillo-Garsow et al., n.d.). Smooth thinking is fundamentally different from chunky thinking, and chunky thinkers will have trouble thinking about change as a continuous process. Contrariwise, thinking in terms of chunks, however, is apparently relatively easy achievable from a smooth perspective (Castillo-Garsow et al., n.d.).

We may briefly summarize what we learned:

• We became even more aware that the power of the context of filling glassware lies in the fact that it offers the students a powerful theory to reason about the covariation process on the basis of their understanding of the relationship between a glass’ width and its speed.
• The students showed their implicit conception of instantaneous speed, when answering the question, “When is the speed in the cocktail glass equal to the speed in the highball glass?”: for this answer presupposes that one thinks of speed in a point.
• The students could handle the tangent-line-tool, but we doubted their level of understanding.
• Further, they still did not manage to come up with a continuous graph; we believe that starting with the highball glass might have put them on the wrong track.

2.3 Design experiment 2

The aforementioned chunky thinking is highly problematic because developing and reasoning about a smooth graph is a key element in the envisioned learning process. To overcome the problem of a discrete learning environment reinforcing discrete thinking, we decided to change the LIT for design experiment 2 to let the students’ learning process revolve around the non-linear situation of filling the cocktail glass. In this we followed Stroup (2002), who argues that linear situations might be too simple to support students developing understanding of calculus-like topics. We also removed the measuring cup activities because these invited students to focus on interpreting a continuous process in a discrete manner.

2.3.1 Modeling-based learning

To increase conceptual discussion about speed we opted for a modeling-based learning approach. Modeling is generally seen as the core activity in science, and a natural element of STEM education. A modeling-based learning approach aims at getting access to the students’ thinking by having them express their understanding in visual or “expressed” models (Coll, France, & Taylor, 2005; Gilbert & Boulter, 1998). An expressed model can be presented, discussed, and evaluated in class, allowing students to refine their models, while giving the teacher (and researchers) indirect access to their thinking. Besides, through this modeling process, a consensus model may come to the fore, which may become taken-as-shared in the classroom.

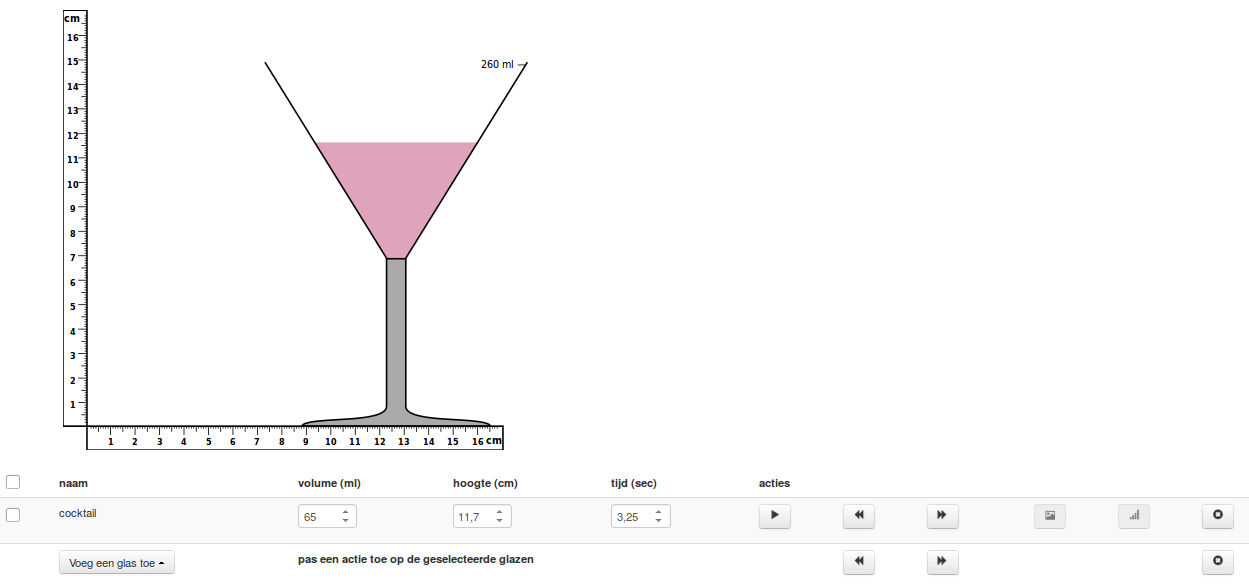
We redesigned the conjectured learning trajectory with a modeling-based learning approach in mind: We would ask the students several times to model the speed with which a cocktail glass fill ups, and to improve their model. We expected the students’ first models to be quite realistic depictions of the situation (Schwarz, 2009), which would be the starting point to support the students in developing more mathematical models. When these first models would be evaluated by running the computer simulation (Figure 6), we expected the students to be surprised by the non-linear nature of the situation, but immediately realize why the glass fills up the way it does. When asked to make a new model, we expected them to express the non-linear nature of the situation by coordinating water height and time. Next, in order to shift the students’ attention toward the quantitative coordination of water height and time, we would ask them to create a model to predict the water height at certain moments. We expected them to create more precise models by using the simulation to measure the water height and time and use these measurements to annotate their models.

Although students were to create more precise models, we did not expect them to start using Cartesian graphs on their own. On the other hand, Galen, Gravemeijer, Mulken, & Quant (2012) showed that children at this age are able to reinvent graphs when supported by a suitable instructional sequence. Once the Cartesian graph was introduced, however, we did expect the students to value it as a useful model. With initial guidance from the teacher, the students could use the graph to predict the water height at any moment. Furthermore, even though they were familiar with straight-lined graphs, once the (computer drawn) graph was introduced we expected the students to connect its shape to their image of filling glassware. They would extend their understanding of the relationship between a glass’ width and speed to include the steepness of the curve: the smaller a glass, the faster the water rises, the steeper the curve. They would realize that the speed changes continuously because the glass’ width changes continuously. However, we did not expect them to be able to determine the speed at a given point.

Then we would shift to a brief exploration of the speed in a highball glass. We expected students to be able to depict filling the highball glass, to explain why it is a straight line, and to compute the constant speed. Next, the students would be guided towards construing the highball glass as a tool for measuring instantaneous speed by exploring when the speed is the same in both glasses.

Building on the realization that when the two glasses have the same width, they would have the same speed, the students were expected to come to see that the cocktail glass’ curve is as steep as the highball glass’ straight line at that point. Finally, we explored if the students could use this understanding in the context of toy-car racing. We expected the students to explain a race given a graph, indicate where the car went fastest or slowest, and use the tangent line to quantify its speed.

2.3.2 Observations, reflections, and revisions

2.3.2.1 Modeling-based learning

We tried this conjectured learning trajectory out in a small-scale teaching experiment with four 5th graders; the first author acted as a teacher. The modeling-based learning approach was a success with respect to generating more conceptual discussion about speed. Modeling helped students and teacher alike to express and discuss their thinking in more detail. There was ample room to explore alternatives. The students had some difficulty with combining the graphs of the cocktail glass and the highball glass. Eventually, they figured out that they had to draw a line through the appropriate point of the cocktail-glass graph, parallel to the highball-glass graph. This offered a basis for introducing the tangent line, and most students were able to determine the instantaneous speeds in the cocktail glass by using the tangent line.

In this manner, the students developed a deeper qualitative understanding, however, their quantitative understanding of instantaneous speed lagged behind. Although they were able to use numerical procedures to compute speed, their ability in applying these procedures was limited. Students’ prior understanding of speed as a ratio of distance over time appeared less well developed than anticipated. Furthermore, students’ command of units and quantities was touch-and-go. We concluded that as primary-school students’ prior understanding is underdeveloped, we would have to pay more explicit attention to units, quantities, and computing speed as part of the learning trajectory.

2.3.2.2 Students appear inherently chunky thinkers

The other main change we had made to the LIT after design experiment 1 did not pan out as we had hoped. We had conjectured that starting the exploration of speed with the cocktail glass and skipping the measuring cup activities would steer students away from discrete thinking and make it easier to interpret filling glassware as a continuous process. However, despite the fact that the students seemed to realize that the speed changed continuously, their models still reflected a discrete perspective. And when the students tried to incorporate more quantitative aspects, their models became even more discrete. This appeared to fit Castillo-Garsow (2012)’s characterization of chunky thinkers. We therefore conjectured that students of this age might be chunky thinkers who have to be supported to in making the switch from discrete to continuous thinking about speed (Castillo-Garsow, 2012).

We may briefly summarize what we learned:

• The modeling activity does help to make the students’ thinking visible and topic of discussion.
• The students show lack of understanding of, and fluency with, measures of speed.
• Still no success in developing continuous graphs: we conjecture that maybe students of this age are chunky thinkers.
• However, the students construed the tangent line to the cocktail glass’ curve parallel to the graph of the highball glass as an indicator of the speed in a given point.

2.4 Design experiment 3

This section, in particular the vignette, is partially based on the results presented in H. de Beer, Gravemeijer, & Eijck (2015).

2.4.1 Working towards continuous graphs

We decided to start again with asking the students to explore the glass-filling context by repeatedly modeling how the cocktail glass fills up. Then, instead of just introducing the curve, we added two activities to support students in developing the continuous graph by building on their own models. First, the students would be asked to draw on paper a minimalistic model by taking one of their previous models as a basis and removing those characteristics that were not absolutely necessary to describe the situation. We expected them to make a step towards more abstract discrete models by removing realistic elements such as glasses and water sources. Then, based on these minimalistic models, the teacher would guide the students to adapt their models to become increasingly graph-like representations, starting with a bar graph, followed by an arrow graph, leading up to a continuous Cartesian graph. The bars in the bar graph would come to signify water heights at specific moments, and arrows connecting these points would come to signify change (Figure 7). In this phase, we expected the graph—as a model—to still derive its meaning for the students from its reference to the actual situation of filling the cocktail glass. Reflecting on computer-drawn continuous graphs and student-generated graphs in relation to the shape of the glass, we expected the students to come to see the curve as signifying both the changing value and the instantaneous speed.

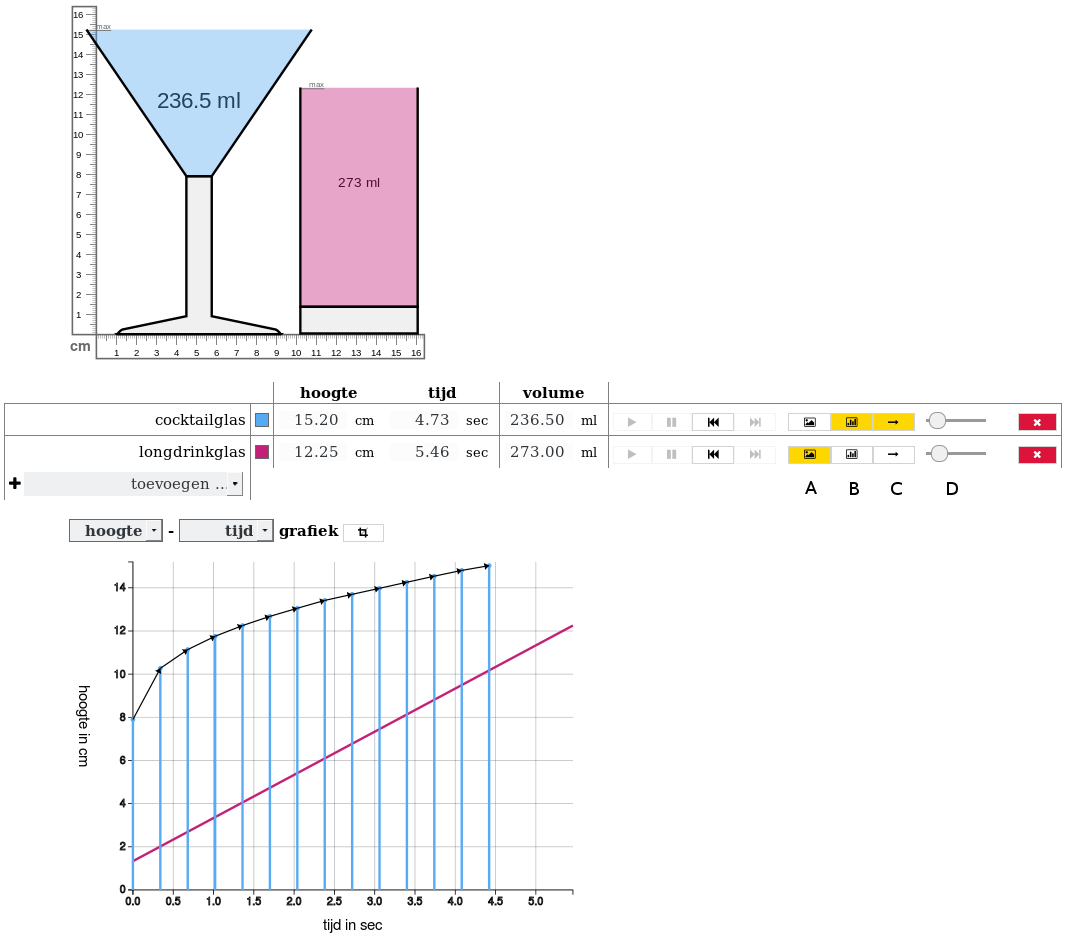
2.4.2 Quantifying speed

Following the introduction of the curve, we would continue with the exploration of quantification of instantaneous speed by introducing the highball glass and asking the students to draw its graph on paper. Here, the teacher would activate the students’ prior knowledge of computing speed by explicitly referring to familiar notions of speed as distance over time before moving towards computing the rising speed in the highball glass. By paying attention to the quantities and the units involved, we expected the students to become better aware of what speed means in this situation. Through exploring speeds in various highball glasses, the students would become familiar with computing speed.

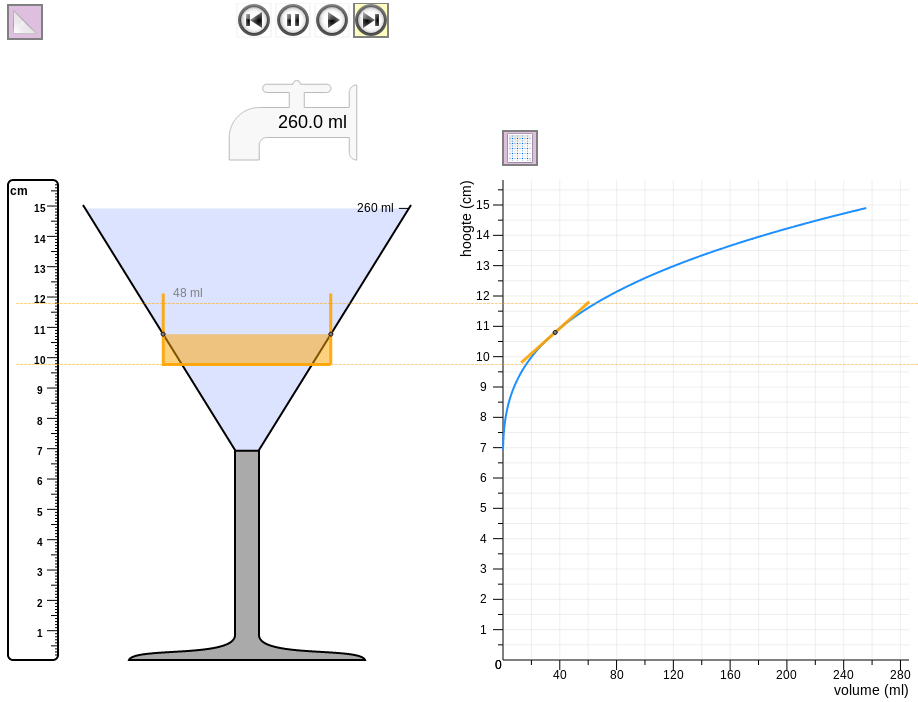
Building on the students’ understanding of the relationship between a glass’ width and speed, they would be guided to invent the highball glass as a tool for determining the instantaneous speed in the cocktail glass. Next, this understanding would be expanded by linking the graph of the highball glass to the steepness of the curve of the cocktail glass at the point where both glasses have the same width. Then the tangent-line-tool would be introduced as a means for measuring instantaneous speed (Figure 8).

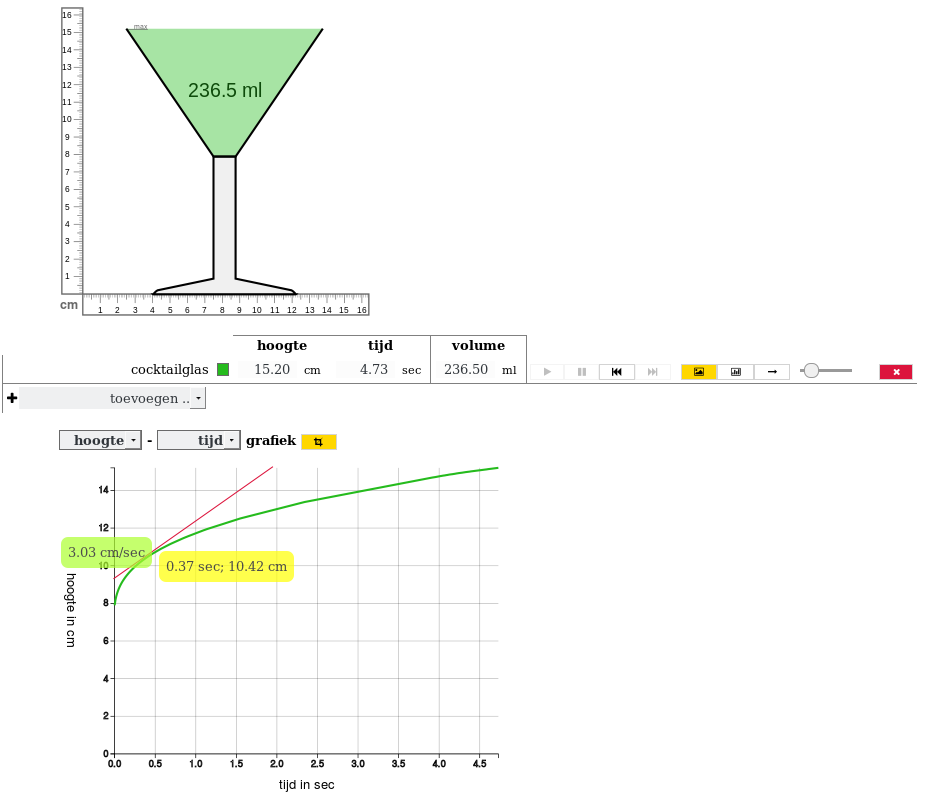
Next, we would switch to the familiar context of cooling down and heating up of water. The students would be asked to graph what happens when a glass of hot water cools down or a glass of ice-water heats up. After discussing these graphs, we would ask students to repeatedly measure the temperature at several moments and to compute the differences with the previous measurement and the room temperature, followed by computing the cooling speed and predicting when the cooling process will be finished. We expected them to improve their first models and to be able to point out where the temperature of the water cools down the fastest and why that is. Thus, we expected them to reinvent a qualitative version of Newton’s law of cooling.

2.4.3 Observations, reflections, and revisions

2.4.3.1 Students constructing continuous graphs

We translated the conjectured learning trajectory into an instructional sequence and tried it in two mixed 4th-6th grade gifted classrooms taught by the same teacher. A month after the first three lessons about filling glassware, a fourth lesson was taught about cooling and heating. Each lesson was first taught in classroom 1 (C1) on Fridays and then, after the weekend, in classroom 2 (C2).

The first lesson went in a similar manner as in design experiment 2: the students created increasingly more discrete models. When the students were asked to create a minimalistic model with only the necessary elements to describe the situation in the next lesson, there was one pair of students in each classroom that created a graph-like model.

In C2, the students did need the guidance of the teacher—as we had anticipated. Building on a discrete visualization of the filling process, the students in C2 became focused on individual water heights—which obscured the bigger picture of how the rising speed changed over time. In C1, however—where a segmented-line graph functioned as a starting point—the students developed an adequate representation of continuously changing speed as an improvement of a given line graph, as shown by the following vignette:

start of vignette

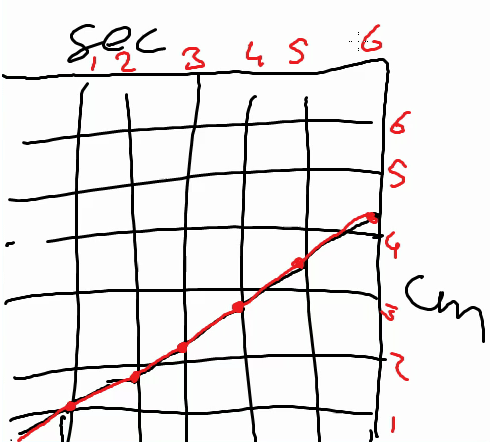
Following the activity to create a minimal model of filling the cocktail glass, the teacher invited several pairs to present their model in front of the class. One of these models was a graph-like model (Figure 10). This involved an exchange in which the students clarified their graph, and the teacher labeled the axes with units and numbers and emphasized the graph by drawing it again in red. Then, after a short detour discussing other students’ models, the teacher returned to the graph-like model and asked a student (Eric) if he could find the rising speed in the graph:

Eric    :   No
Teacher :   Why not?
Eric    :   Because it's slanted and it's slanted like that the whole time.
Teacher :   And that fits with this, with this, this glass?
Eric    :   No.
Teacher :   No, right? And how should it go then, you think? Eric, or Larry
Larry   :   I think it should go a bit bent

While drawing a curve in red on top of the graph (see Figure 11), Larry explained that at a certain moment the graph almost does not rise any more. When the teacher asked if everyone understood what Larry was doing, they answered yes; Jessica explained:

Jessica :   Yes, because it is bent, you can have it go, yes, steeper, 
            so you can specify that it goes slower all the time. Because
            in the end, it has to go to the right.
Teacher :   But, where, where, in what part of the graph it rises the 
            fastest, for example?
Timothy :   In the beginning, at the bottom
Teacher :   Yes, in the beginning, here at the bottom. But why, how can you
            see that?
Timothy :   Well, beacuse there, it goes up.
Teacher :   But here (teacher points to a part of the graph at two thirds of
            the length of the graph) it does also go up
Timothy :   Yes, but it goes a little less higher
Teacher :   Less higher?
Timothy :   Yes, less fast

end of vignette

2.4.3.2 Students are smooth thinkers, but fall back to discrete models

We explored this unexpected difference between the two classrooms in detail in H. de Beer et al. (2015), where we concluded that although classroom conditions often gave rise to the invention and use of discrete representations, the underlying conception that the students reasoned from was continuous. Various facts substantiated our conjecture that the students came to the classroom with a continuous conception of speed. First, the students quickly realized that the speed was continuously decreasing because of the growing width of the cocktail glass’s bowl, when they saw a cocktail glass fill up. Second, the students spoke about their realistic drawings or snapshots models as descriptions of a process. Third, the ease with which the students came up with snapshots suggested that students were familiar with the idea of using discrete snapshots to visualize change over time. Fourth, the students effortlessly accepted the curve, once it was introduced, which could be explained by assuming that the continuous model matched their existing continuous conception of the situation. Fifth, after having seen how a discrete graph approached a curve when decreasing the interval between points, the students never referred back either to the bar graph or the arrow graph in later lessons. Finally, the students in classroom C1 developed a continuous curve by themselves because they were dissatisfied with the discrete and linear graph.

2.4.3.3 Procedural understanding and quantification

With regard to students’ superficial notion of quantification, the teaching experiment of design experiment 3 further showed that the students were able to quantify speed with the help of the teacher. However, their quantitative understanding never seemed to exceed the ability to execute a procedure to compute speed. Apparently, the quantities, the units, and the measurements were not meaningful to them, and did not transcend the level of numbers in a calculation.

Finally, with respect to the flexibility of the students’ understanding of instantaneous speed, the way the students reasoned in the context of cooling and heating was similar to that in the context of filling glassware. They were able to represent their understanding of a situation in a graph and could interpret a graph in light of the situation. They were able to point out when the speed was highest or lowest, and could use the tangent-line-tool to measure instantaneous speed.

We may briefly summarize what we learned:

• The students in C1 were able to invent a continuous graph by themselves, by using their understanding of the relationship between a glass’ width and speed, and thus of the character of the covariation. Therefore, they are not chunky thinkers; they are continuous thinkers who have difficulty with graphing!
• Although starting discrete, the students in classroom C2 came to understand the continuous graph via shrinking the intervals of a bar chart.
• The students construed the tangent line as an indicator of the speed at a given point. (We see this as a tangent line; the students however were not yet familiar with that notion.)
• Students came to understand the shape of the graphs of a cooling process as being predicted by the tangent line that is depended on the temperature differences.
• Students did not have a sound basis for calculating speeds: they did not really understand average speed, and they had a limited understanding of the measurement units. They need more experience with quantifying constant speeds in a variety of ways (with different units), and relating those with the corresponding graphs.

3 The yield and trackability of our learning process

We may argue that the instructional sequence we tried in the last teaching experiment worked rather well. Although the students’ weak understanding of measuring speed clearly was a limiting factor. On the other hand, the invention of the curve as a better representation of the process of filling a cocktail glass surpassed our expectations. If we adjust for these two aspects we may describe the prototypical instructional sequence emerging from the last teaching experiment as follows:

1. Students model the process of filling a cocktail glass.

2. Supported by a computer simulation, students develop a minimalistic model of this process on paper. This explicates the underlying process: the wider the glass, the slower the water level rises.

3. Students work towards conventional graphs that are known to them: bar graphs and segmented-line graphs.

4. Students are supported in inventing the continuous and curved line graph as the best representation of the cocktail glass’ filling process by a) critiquing the segmented graph and b) increasing the number of bars in the bar graph with a computer tool.

5. Students explore the highball glass, its linear graph, and its constant speed with the computer tool (that can show a simulation of the filling process, and has the option of showing the corresponding graph); by investigating highball glasses with various widths, and by varying the measurement units.

6. Students discuss the question: “When are the speeds in a cocktail glass and a highball glass the same?”

7. Students are introduced to and work with a virtual highball glass in the computer simulation.

8. Students compare the graphs of the cocktail glass and the highball glass; they figure out that a straight line that touched the cocktail glass’ curve at the point where the widths of both glasses are the same is parallel to the highball glass’ graph, and it signifies the speed in that point.

9. Students investigate the tangent line as an indicator of speeds in various points of a graph; both static, in a given point, and dynamic, moving along the graph.

10. Students generalize their understanding of instantaneous speed and graphs towards the context of heating and cooling of water.

The development of this prototypical instructional sequence was illustrated in the previous section in terms of our own learning process, which encompassed both the design decisions and the rationale for those decisions, and thus also described the emerging LIT. To avoid too much overlap, we will not reiterate this LIT here in detail, but summarize the most important theoretical findings. We formulate such a LIT elsewhere in detail (H. de Beer, Gravemeijer, & Eijck, 2017), however.

1. Key is the thesis that the students are spontaneously thinking in terms of instantaneous speed from the start. This conception allows the students to come up with “equal widths” as the answer to the question, “When is the speed in the cocktail glass and the highball glass the same?” This also fits with the students’ quick understanding of the constantly decreasing speed in the cocktail glass, and with the intuitive appreciation of the curved continuous graph. It also enabls the students to reinvent the continuous graph by arguing that the graph of filling a cocktail glass can not be linear because the rising speed is diminishing all the time. Thinking of speed as instantaneous speed, and realizing that the speeds are the same at the point were two glasses have the same width, enables them to use the virtual highball glass as a means of establishing the speed at a given point in a cocktail glass.

2. When asked to turn a highball glass into a measuring cup, the linearity of the relationship between water level height and volume is self-evident for the students. Having made such a measuring cup, they effortlessly express the imaginary process of the glass filling up with a linear graph. As the students have little understanding of average speed, we may assume that they think of constant speed in connection with a linear process. This understanding is powerful enough to help the students construe the tangent line as an indicator of the speed in a given point: by combining the cocktail glass’ graph and the graph of the virtual highball glass. Unfortunately, their understanding of, and fluency with measures for speed hinders the opportunity to subsequently quantify instantaneous speed. However, they understand the tangent-line-tool well enough to link the difference between the actual and the final temperature to the tangent line in a cooling or heating process, and explain the cooling (respectively heating) graph in this manner.

These theoretical findings offer the rational underpinning the prototypical instructional sequence. They can be taken as conjectures on how students in other classrooms may reason. In this manner, they offer a framework of reference on the basis of which teachers may adapt the instructional sequence to their own needs and their own classroom. In addition, they offer support for instruction design, and for new design experiments and further theory development.

3.1 Empirically-grounded theory

In order to function in this manner the aforementioned theories have to be substantiated. Following Smaling (1990) we argued earlier that the theoretical findings could be substantiated by the virtual repeatability of one’s research by other researchers. In relation to this, we have to bear in mind that design research differs from more classical forms of research in what it tries to achieve. A standard goal for classical educational research is to establish whether intervention A works better than intervention B. The goal of design research, however, is quite different. Here the goal is to generate a theory on how the intervention works. This distinction may be linked to two conceptions of causality, as described by Maxwell (2004): a regularity-oriented causality, and a process-oriented causality, respectively.

The former, which looks at the frequency with which an assumed cause is followed by a presumed effect is typical for quantitative research in education. In contrast, the kind of research we are discussing here employs a process-oriented perspective on causality, which ‘deals with events and the processes that connect them; it is based on an analysis of the causal processes by which some events influence others.’ (Maxwell, 2004, p. 5) It is based on the idea that causation is a complex process that is dependent on a combination of variables and circumstances. In principle, causal claims could be based on a single case. When aiming at LITs, a single case will not be just one student. Instead, the classroom as a whole will be the unit of analysis. As a result, to justify that there is a causal relation, narrative explanations can be used (Abell, 2004). Applied to educational settings, Maxwell (2004) argues that ‘[t]o develop adequate explanations of educational phenomena (…), we need to use methods that can investigate the involvement of particular contexts in the processes that generate these phenomena and outcomes.’ (p. 7) We may argue that design research deploys two such methods: validating existing conjectures and generating new explanatory conjectures.

3.2 Validating and generating conjectures

In each design experiment, the conjectures about the learning process and the means of support are substantiated in the instructional activities and materials that are developed, tried out, adapted, and refined in multiple micro-design cycles during the teaching experiments phase of the design experiment. Conjectures that are confirmed by the students’ actual learning process remain part of the LIT and are tried and refined again in the next design experiment. As a result, conjectures are confirmed or rejected in multiple different situations, offering a form of triangulation that adds to our understanding of students’ learning processes in terms of these conjectures. Those observations enabled us to develop some theories about the mechanisms that were at play here.

In addition to this, new explanatory conjectures are generated through abductive reasoning, which is to ‘rationalize certain surprising facts by the adoption of an explanatory hypothesis’ (Fann, 1970), allowing us to focus on causal processes that we did not anticipate in the LIT. A surprising fact is an indication that our understanding of the students’ learning processes did not match the actual students’ learning processes; it suggests a gap in our theory. To fill that gap, we select data during the retrospective analysis that allows us to focus on what happened during the unexpected event to explore plausible hypotheses of why it happened. By detailing our learning process, we may show why and how we generated new explanatory conjectures.

Our learning process described in the previous sections shows a chain of reasoning throughout the subsequent design experiments focusing on the dichotomy between students’ discrete and continuous reasoning and the lack of conceptual whole-class discussions about speed. In design experiment 1, students reasoned about the continuous changing non-linear situation of the cocktail glass from a discrete perspective. While exploring what happened, we also found that there was a lack of conceptual discussion about speed, adding to our difficulty explaining why students reasoned from a discrete perspective. We found a plausible hypothesis in Castillo-Garsow’s (2012) distinction between chunky and smooth thinkers: and we conjectured that the students’ discrete thinking was reinforced by a discrete learning environment. We decided to adapt the initial LIT in design experiment 2 by offering students a continuous learning environment, while using a modeling-based learning approach to graphing to provoke conceptual discussion.

Through the modeling-based learning approach we gained more insight in students’ conceptions about instantaneous speed. However, our adaptation of the learning environment by focusing on exploring the process of filling the cocktail glass, proved less effective. During the first modeling activities, students created increasingly discrete models and, although one pair of students introduced a graph-like model that the other pair appropriated in a later activity, students had trouble to link the curve to their developing understanding of speed. This suggested that the students were chunky thinkers (Castillo-Garsow, 2012) who saw change as fundamentally discrete in nature and need support switching to a continuous perspective.

We adapted the LIT in design experiment 3 by introducing an activity where students would, guided by the teacher, rediscover the curve step by step while building on their own models. Whereas this anticipated learning trajectory was followed in one classroom, in the other, the students themselves constructed the curve. This made us reconsider what we knew about the students’ use of the word “speed”, and we realized that we implicitly assumed that the students were thinking of average speed when they talked about speed. This led us to reexamine our data on the students’ conceptions of speed, which lead to the conclusion that they did not speak of, or reason with, average speed. Instead, our analysis showed that they reasoned from an informal conception of instantaneous speed. Thus their intuitive notions of speed were continuous, but they lacked the representational competency to model it with continuous models, and therefore resorted to discrete snapshots models (H. de Beer et al., 2015).

The above shows how surprising facts evoked abductive reasoning, which generated potential explanations which could be tested on the available data.

4 Discussion

Even though some of those findings reflect what is already known about what students can do and how they are taught in regular classrooms, we believe that the findings as a whole offer a new and exciting perspective on what and how primary-school students learn about speed. Their insight in what determines the rising speed in a glass, and their implicit conception of speed as an instantaneous speed that may change continuously, can be exploited by supporting various forms of graphing, in order to develop a deeper understanding of speed that may evolve into understanding speed as a rate.

As a caveat we may note that these claims are based on observations of how the students acted and reasoned during the design experiments. While our interpretations of those observations fed into either the next activity or the next experiment, which resulted in micro-design and macro-design cycles that had strong similarities with an empirical cycle of hypotheses testing. We can, however, only make claims about the students who participated in our experiments. Even then we have to take care to carefully ground our claims in the observational data. That is, we have to make sure that our conclusions are valid for the majority of the students and not just a few, which is not always easy as not all students speak up during classroom discussions. Here it is important to determine what the social norms in the classroom are. We have to know, whether the students feel obliged to speak up when they disagree or do not understand what is going on. We judged that this was predominantly the case in the classrooms where the experiments were carried out.

In addition to the micro-design cycles that immediately contribute to the learning process of the researchers, one usually also carries out a retrospective analysis after the experiment is concluded. Here Glaser and Strauss’ (Glaser & Strauss, 1967) method of constant comparison is the designated method. We especially applied this method in the third teaching experiment. Basically this method boils down to (a) developing conjectures about what happened during the experiment, and test those against the available data, and (b) developing conjectures about why this happened, and test those conjectures against the available data.

Mark that the results of this procedure limit themselves to statements about the actual design experiments. Glaser and Strauss’s (1967) method does not answer the question whether those results are generalizable. On the basis of those findings, however, a design experiment can be treated as a paradigm case. The goal then is to come to understand (the role of) the specific characteristics of the investigated learning ecology in order to develop theoretical tools that make it possible to come to grips with the same phenomenon in other learning ecologies. Instead of a scripted lesson plan, the LIT offers a theory of how the intervention works, which teachers and instructional designers can adjust and adapt. To be complete, we should add that design research may also aim at developing theories—or theoretical tools—on more encompassing issues that transcend the LIT, such as ‘classroom social norms’, or ‘symbolizing’. In such cases, the learning ecology, which is created, serves as a condition for research on this more encompassing issue.

4.1 Educational design and design research

Finally, we want to discuss the relationship between educational design and design research we touched upon in the introduction. Design research uses educational design as a tool to realize a learning ecology that is conductive to exploring students’ learning processes in detail. In particular, educational design comes to the fore during the teaching experiment phase of a design experiment. In this phase an educational design is created on the basis of a conjectured LIT: In multiple micro-design cycles, instructional activities are developed, tried in a classroom setting, evaluated, adapted, and refined. In this phase, although the LIT is leading, the emphasis is on providing meaningful instruction to the students. Ultimately, however, although design research does produce an instructional sequence, design research aims at developing a LIT that explains how that instructional sequence works in terms of students’ learning processes.

The instructional sequence does not often evolve beyond a prototype in design research (Burkhardt & Schoenfeld, 2003), which implies that it cannot directly put into practice. From a design research perspective, the theory that is produced is more important, as it may inform researchers, educational design practitioners, and teachers about students’ learning in a particular domain and means to support that learning (Gravemeijer & Cobb, 2013). However, from a practical point of view, the potential utility of the LIT is most apparent through the plausibility and support of the instructional sequence. This difference in aim, theory or practice, lies at the heart of the divide between the communities of design research and educational design (Schoenfeld, 2009). We think that design research practitioners can help bridging this gap by contributing to the codification of design practice called for in the educational design community (Schoenfeld, 2009; Schunn, 2008). In this respect we may point to the theory of realistic mathematics education (RME). RME is developed by generalizing over LITs (Treffers (1987)], and can be recast in terms of a set of instructional design heuristics (Gravemeijer, 2008).

To develop theory implies a commitment to the credibility of the LIT by justifying the claims made in it and a commitment to allow other researchers to assess the trustworthiness of the process leading up to those claims. The latter commitment can be satisfied by virtual replicability or trackability (Smaling, 1990), which means giving a detailed account of the design research process and the researchers’ own learning process embedded in it. This will encourage design researchers to pay attention to practical issues of design. Hopefully, this will allow design researchers to create theories that are more practical applicable.

On the other hand, design research can be taken as a paradigm that may show educational designers the value of documenting design decisions and anticipated students’ learning processes. Similar to design researchers, they may start describing their learning processes by making their design decisions explicit when preparing for an educational design project. While also explicating how these decisions build on existing theory as found in the literature. Furthermore, during the retrospective analysis, they may document how they evaluated what happened during the teaching experiments what they did to optimize the design, and how they thought about why the design worked the way it did. From this perspective, design research can be seen as an augmented form of educational design, which offers educational designers indications on how to handle the issue of documenting their practices and knowledge.

Bibliography