An image of Heer de Beer

Heer de Beer.org

Exploring the Computational Medium

Docentenhandleiding — Snelheden met computers en grafieken

Huub de Beer

Conceptversie 0.1 — 2013-08-06

1 Inleiding

2 Planning

  1. Voorbereiding

    1. praktische voorbereiding
    2. inhoudelijke voorbereiding

  2. Deel A: De stijgsnelheid van het waterniveau in een glas

    • 2 lessen te verdelen over meerdere lessen

  3. Intermezzo reflectie en opzetten deel B

  4. Deel B: Afkoelingssnelheid en isolatie

    • 2 lessen te verdelen over meerdere lessen

  5. Evaluatie

3 Achtergrond

3.0.1 Informatiesamenleving

Een van de kenmerken van de moderne informatiesamenleving is de grote hoeveelheid gegevens die we met zijn allen genereren. Van een klein deel van deze gegevens zijn we ons bewust. Zo communiceren we met elkaar via sociale media en laten veel berichtjes achter. We reizen met de OV-chipkaart en checken steeds in en uit. We verkennen het internet en alle adressen die we bezocht hebben, vinden we terug in onze browsergeschiedenis. We pinnen in de winkel en zien deze transacties terug in het digitale overzicht bij het internetbankieren. Enzovoorts.

Maar van het overgrote deel van de gegevens die in de informatiesamenleving worden gegenereerd, zijn we ons niet of nauwelijks bewust. Van bijna elk systeem of proces wordt informatie bijgehouden, en dat vaak real-time. Denk aan het loggen van toegang tot gebouwen en ruimten, het insturen en verwerken van formulieren, het aansturen en monitoren van productieprocessen, het meten van het weer, sensoren in moderne auto’s houden de prestaties van de moter in de gaten, enzovoorts.

Niet alleen genereren we met zijn allen steeds meer gegevens, we krijgen er ook steeds meer toegang toe doordat informatiesystemen aan het internet worden aangesloten. Door greep te krijgen op deze gegevens, door er informatie van te maken, krijgen we greep op de wereld om ons heen. We maken informatie van gegevens door interpretatie en representatie van die gegevens. Om leerlingen voor te bereiden op participatie in de moderne informatiesamenleving is het belangrijk dat ze leren om gegevens te representeren en te interpreteren.

3.0.2 Interpreteren en representeren van dynamische systemen

In deze lessenserie beperken we ons tot het onderzoeken van eenvoudige dynamische systemen zoals afkoeling van een kop thee, de groei van een zonnebloem, of het vullen van een glas met water. Dynamische systemen spelen een belangrijke rol in onze technologisch hoogwaardige informatiesamenleving en vormen een belangrijk onderzoeksonderwerp in de meeste natuurwetenschappelijke en technische vakgebieden zoals de natuurkunde, werktuigbouwkunde, scheikunde, biologie, elektrotechniek, wiskunde en zelfs economie. Het is dan ook niet verwonderlijke dat we continue in aanraking komen met allerlei dynamische systemen, meestal zonder ons daarvan bewust te zijn. Als gevolg hiervan hebben leerlingen al een intuïtief begrip van veel eenvoudige dynamische systemen.

Een dynamisch systeem wordt gekarakteriseerd door de verandering van enkele grootheden gedurende een bepaalde periode. Twee grootheden waarvan de verandering samenhangt, vormen samen een nieuwe samengestelde grootheid die de snelheid beschrijft waarmee de ene grootheid verandert gegeven de verandering van de andere grootheid. In de meeste dynamische systemen zijn dergelijke snelheden niet constant en ze veranderen continue. We noemen zo’n snelheid dan een momentane snelheid.

Zo daalt bij het voorbeeld van het afkoelen van een kop thee, de temperatuur van het theewater terwijl de tijd verstrijkt. De snelheid waarmee de thee afkoelt, uitgedrukt in graden Celsius per seconde, daalt ook. Hoe groter het verschil tussen de buitentemperatuur en de temperatuur van het theewater, hoe sneller het water afkoelt.

Het dynamische systeem van dit voorbeeld kunnen we onderzoeken door een temperatuursensor in een kop thee te hangen en die sensor uit te lezen met behulp van een computer. De sensor meet de temperatuur continue en de computer leest om de zoveel milliseconden de temperatuur uit. Dit levert een grote lijst op van opeenvolgende momenten en de op dat moment gemeten temperatuur. Door te proberen greep te krijgen op die gegevens, krijgen we greep op het onderliggende dynamische systeem. Echter, om die gegevens te interpreteren hebben leerlingen een meer wiskundig begrip van verandering in dit soort dynamische systemen nodig.

Deze wiskunde wordt traditioneel onderwezen in de bovenbouw van havo/vwo en in het hoger onderwijs en staat bekend als wiskundige analyse of de differentiaal- en integraalrekening. De basis van wiskundige analyse is de algebra. Algebra is geen onderdeel van het curriculum Rekenen-Wiskunde op de basisschool. Dat maakt deze wiskundige analyse ongeschikt voor het basisonderwijs.

Aan de andere kant biedt de moderne informatietechnologie jongere leerlingen de mogelijkheid om dynamische systemen te onderzoeken, bijvoorbeeld met behulp van interactieve computersimulaties van dergelijke systemen. Daarbij is het voor de leerlingen niet nodig om gebruik te maken van algebra (Kaput & Schorr, 2007; Stroup, 2002; Thompson, 1994).

In de lessenserie grijpen we terug op de definitie van momentane snelheid die Willem van Heytesbury in 1335 op schrift stelde:

‘Een momentane snelheid van een bewegend voorwerp meten we als de afstand die dat voorwerp zou afleggen als het gedurende een tijdseenheid met die snelheid zou voortbewegen zoals het op dat moment doet.’ (geparafraseerd uit: Heytesbury (1335) Regule solvendi sophismata, zoals geciteerd in (Clagett, 1959, pp. 235–237))

Deze definitie uit de geschiedenis van de begripsontwikkeling van momentane snelheid past beter bij het intuïtieve begrip dat basisschoolleerlingen hebben van momentane snelheid dan de standaard wiskundige definitie uit de differentiaalrekening. Basisschoolleerlingen hebben immers al een intuïtief begrip van momentane snelheid. Het grootste deel van hun leven ervaren ze immers allerlei dynamische fenomenen, van het naar school fietsen tot het spelen van computerspellen. We verwachten dat de leerlingen in staat zijn om een dieper wiskundig begrip van momentane snelheid te bouwen op basis van hun intuïtieve begrip van snelheid.

3.0.3 Snelheid in het basisschoolcurriculum

Het begrip “snelheid” is geen nieuw onderwerp op de basisschool. Het wordt bijvoorbeeld expliciet genoemd in kerndoel 33 (Rekenen/wiskunde):

‘33 De leerlingen leren meten en leren te rekenen met eenheden en maten, zoals bij tijd, geld, lengte, omtrek, oppervlakte, inhoud, gewicht, snelheid en temperatuur.’ (SLO, 2006, p. 11)

De Stichting Leerplanontwikkeling (SLO) werkte dit leerdoel op hun website TULE verder uit. In groep 5/6 verkennen de leerlingen ‘de grootheid snelheid en een van de meest gangbare maateenheid daarvoor: km/u’. In groep 7/8 verkennen leerlingen de relatie tussen tijd en ‘andere grootheden, met name (…) snelheid (km/u)’ en ze leren ‘werken met het begrip snelheid; verkenning van het omrekenen van km/u naar m/sec, en omgekeerd’.

In een meer uitvoerige uitwerking (Buijs, Klep, & Noteboom, 2008) benoemde het SLO daarbij de volgende activiteiten voor leerlingen:

Het begrip van “snelheid” dat leerlingen op de basisschool zouden moeten ontwikkelen dat hieruit naar voren komt, is:

Er wordt nadrukkelijk niet gerept over momentane snelheid, noch over andere snelheden. (Er wordt een andere samengestelde grootheid genoemd, dichtheid, maar dat is, zeker in het basisonderwijs, typisch een niet-veranderlijke grootheid)

In onze vorige experimenten ondervonden we dat dit formele snelheidsbegrip bij leerlingen vooral oppervlakkig van aard was. Leerlingen waren in staat om snelheden van de ene eenheid om te rekenen naar de andere. Ze begrepen snelheid niet als een samengestelde grootheid, maar als een enkelvoudige grootheid van snelheidlengten (vrij naar “speed-lengths” in (Thompson & Thompson, 1994)): omdat snelheid constant is, kan snelheid beschouwd worden als een afstand dat een bepaalde vaste tijd kost om af te leggen.

Daarnaast zijn er in eerdere onderzoeksprojecten (Galen & Gravemeijer, 2010; Galen, Gravemeijer, Mulken, & Quant, 2012) lessen uitgevoerd ter verdieping van het begrip snelheid en veranderlijke samengestelde variabele grootheden anders dan voortbeweging.

3.1 Onderwijsvorm — Modellerend leren

De gekozen onderwijsvorm is het zogenaamde modellerend leren (modeling-based learning in het Engels). Modellerend leren is een vorm van onderzoekend leren. In plaats van “onderzoek doen” wordt “modelleren” gezien als de kern van wetenschap en ontwikkeling van wetenschappelijke kennis. Vanuit dat perspectief word modelleren gezien als de logische basis voor wetenschap- en techniekonderwijs.

Bij “model” denken we meestal aan maquettes, 3D-modellen, Madurodam, en andere concrete tastbare schaalmodellen. Maar er zijn veel meer soorten modellen die we regelmatig tegenkomen, bijvoorbeeld (J. Gilbert, 2004; S. Gilbert, 1991):

Maar het opnoemen van soorten modellen vertelt ons nog niet wat een model eigenlijk is. Een model beschrijft datgene dat we beter willen begrijpen in termen van iets dat wel al goed begrijpen. Zo’n model is allereerst een mentaal model dat iemand zich vormt van een of ander fenomeen dat onderzocht wordt. Anderen hebben geen toegang tot dit model. De enige mogelijkheid om onze ideeën met anderen te delen is door het mentale model op een of andere manier uit te drukken. Zo’n model noemen we een uitgedrukt model. Zie ook onderstaand Figuur (op basis van (Coll, France, & Taylor, 2005; J. Gilbert & Boulter, 1998)):

datgene dat we beter willen begrijpen mentaal model uitgedrukt model consensus model
Modelleerproces in een leergemeenschap

Zo’n uitgedrukt model kan geëvalueerd en besproken worden in een groep. Deze discussie zorgt ervoor dat de groepsleden hun mentale model verfijnen om vervolgens het uitgedrukte model weer aan te passen. Zo ontstaat er in die groep een zogenaamd consensus model van datgene dat we beter willen begrijpen.

In de wetenschap en techniek worden modellen veel gebruikt, ontwikkeld en verfijnd. We noemen dergelijke modellen uit de wetenschappelijke gemeenschap wetenschappelijke modellen. Wetenschappelijke kennis wordt ontwikkeld door dit modelleerproces.

Het doel van modellerend leren is nu (Coll et al., 2005; Coll & Lajium, 2011; J. Gilbert, 2004; Lehrer & Schauble, 2010; Louca & Zacharia, 2012):

Maar (Lehrer & Schauble, 2010) waarschuwen dat modelleren niet vanzelfsprekend is. Het is een vaardigheid die de leerlingen, docent en de klas als geheel zal moeten ontwikkelen. Modelleren leren we door actief te participeren in een modellerende leergemeenschap waar kritisch naar modellen gekeken kan worden.

Toepassen van modellerend leren houdt dan ook in dat er nadrukkelijk aandacht aan het modeleren zelf besteed moet worden.

4 Deel A - Vullen van glazen en flessen — stijgsnelheid

4.1 Inleiding

Tweeledig doel: ontwikkeling modelleervaardigheid en verdieping begrip verandering en snelheid in de context van het vullen van glazen, en dan met name het begrip momentane snelheid.

4.2 Modelleer de stijgsnelheid in het cocktailglas

De eerste les staat in het teken van het modelleren van het huidige begrip van stijgsnelheid in het cocktailglas, het vervolgens wiskundig verdiepen van dat begrip en het ontwikkelen van modelleervaardigheid.

4.2.1 Benodigdheden

4.2.2 Introductie

We beginnen deze les met de introductie van het cocktailglas om vervolgens de les te besteden aan het modelleren van de stijgsnelheid van het waterpeil in dat cocktailglas. In de eerste opdrachten vragen we de leerlingen om in te beelden wat er gebeurt met de stijgsnelheid bij het vullen van het cocktailglas. Leerlingen zijn beter in staat zich deze situatie in te beelden als ze de cocktailglazen in hun handen hebben gehad.

4.2.3 Leerlingen maken hun eerste modellen “uit het hoofd”

We beginnen met het modelleren van de stijgsnelheid individueel, om vervolgens in tweetallen de modellen te bespreken en gezamenlijk een nieuwe te maken. Eventueel herhalen we dit proces in groepjes van vier. We willen ervoor zorgen dat elke leerling inbreng heeft in de modellen. Probeer daarom die leerlingen bijeen te zetten die verschillende soorten tekeningen hebben gemaakt zodat discussie mogelijk is. Stimuleer vervolgens deze discussie.

Omdat modelleren een nieuwe activiteit is voor de leerlingen kan het voorkomen dat een enkele leerling geen enkel idee hebben wat ze moeten doen en niets tekent. Dit probleem wordt versterkt doordat deze eerste activiteit een erg vrije activiteit is. In zo’n geval kan de leerling ondersteund worden door hem/haar te vragen te beschrijven (verbaal) wat er gebeurt als je water in een glas giet. In een dialoog met de leerling kunnen ideeën ontwikkeld worden hoe die beschrijving getekend zou kunnen worden.

individueel

  • Schrijf je naam op het antwoordvel.
  • Beeld je in wat er gebeurt bij het vullen van het cocktailglas.
  • Maak vervolgens een tekening van de stijgsnelheid van het water in het cocktailglas. Je tekent wat jij denkt en begrijpt van de stijgsnelheid. Elke tekening is dan ook goed.
  • Probeer de tekening zo te maken dat je aan een andere leerlingen uit kunt leggen wat de stijgsnelheid is.

in tweetallen

  • Jullie krijgen elk ongeveer twee minuten om aan de hand van je tekening de ander uit te leggen wat de stijgsnelheid in het cocktailglas is. De linkerleerling begint met uitleggen.
  • Schrijf jullie namen op het antwoordvel.
  • Maak nu samen een nieuwe tekening van de stijgsnelheid in het cocktailglas. Zorg ervoor dat jullie beiden tevreden zijn met de tekening en uit kunnen leggen aan andere leerlingen wat volgens jullie de stijgsnelheid is.

We verwachten dat leerlingen de stijgsnelheid in het cocktailglas modelleren door een tweedimensionale tekening van het cocktailglas te maken, voorzien van een waterbron en al dan niet gedeeltelijk gevuld met water (zie Figuur 3). Ze maken een tekening van de situatie zoals ze dat zien (of het zich inbeelden), maar ze nemen in de tekening niet op wat ze wel begrijpen van de situatie maar dat ze niet direct kunnen zien. Misschien dat een enkele leerling met tekst of pijlen aangeeft hoe het water stijgt of wat er gebeurt met de stijgsnelheid.

Het probleem van het modelleren van een dynamische systeem is dat het (continue) verandert. Hoe kun je die verandering aangeven? Leerlingen geven die verandering aan met behulp van snapshots (Zie Figuren 2, 3 en 4).

De tweede opdracht resulteerde in modellen die aspecten bevatte van elk van de modellen van de individuele leerlingen. Werkend in tweetallen schreven de leerlingen meer bij hun modellen. Dit is waarschijnlijk het resultaat van het gezamenlijk overleggen en expliciet verbaliseren van hun mentale modellen. Tegelijkertijd kozen de tweetallen ervoor om geen expliciete momentopnamen te tekenen en geen getallen bij hun modellen te schrijven.

Bij het presenteren van hun modellen en het overleggen bij het gezamenlijk tekenen van een nieuw model, verwezen de leerlingen regelmatig naar de relatie tussen de stijgsnelheid en de breedte van het glas. Het begrip van de leerlingen van de stijgsnelheid in deze situatie lijkt dieper dan hun eerste modellen doen vermoeden.

Let hierop tijdens de klassediscussie: probeer hun mentale model en hun uitgedrukte model te laten convergeren. Dit convergentieproces kan ondersteund worden door bij het evalueren van de modellen de leerlingen die alternatieven te selecteren die het beste aansluiten bij hun mentale modellen.

4.2.4 Evalueer en verfijn het model aan de hand van de simulatie

Wat een goed model is, is iets dat de docent, de leerlingen en de klas als geheel ontwikkeld. Ben eerlijk, kritisch, maar bovenal onderbouw met argumenten waarom iets goed of niet goed is. Dit is vergelijkbaar met of onderdeel van de ontwikkeling van sociomathematical norms in een klas (Yackel & Cobb, 1996).

Inventariseer en bespreek de verschillende modellen.

  • Laat per soort model een groep hun model presenteren

  • Evalueer het model met de klas:

    • Welk aspect wordt “beter” gemodelleerd? Waarom?
    • Welk aspect wordt niet of minder “goed” gemodelleerd? Waarom?

    Zorg ervoor dat leerlingen hun kritiek onderbouwen met argumenten. Sommige argumenten zijn in sommige contexten meer relevant dan andere. Vergelijk:

    • mooi — nauwkeurig
    • in een tekening — in woorden
    • een momentopname — gehele proces
    • snelheid — hoogte
    • grootheden coördineren — focus op een grootheid
    • enzovoorts

  • Probeer dieper in te gaan op waarom het water sneller stijgt als het glas smal is en langzamer als het breed is. Komt dat naar voren in de modellen? Hoe zouden we die relatie kunnen modelleren? Verschillende alternatieven zijn mogelijk.

Om de leerlingen te ondersteunen bij het tekenen van hun modellen zijn er een aantal standaard modelbasis antwoordbladen gemaakt (zie Bijlagen):

Door deze antwoordbladen te gebruiken, zijn de leerlingen vrijgesteld van het secuur tekenen van de cocktailglazen of grafiekbasis en kunnen dan hun focus richten op het modelleren van de stijgsnelheid. Leerlingen krijgen dan de ruimte om hun model in meer detail te bekijken en eventuele “afwijkingen” (in de ogen van de leerlingen) aanpakken. De leerlingen normaliseren (Ainley, Pratt, & Nardi, 2001) daarmee de modellen naar hun maatstaven en geven zichzelf als het ware feedback. Zorg er wel voor dat de leerlingen zelf expliciet de keuze maken om een modelbasis te gebruiken.

We verwachten dat de meeste leerlingen begrijpen dat het vullen van het cocktailglas geen lineaire situatie is waarin het water met constante snelheid stijgt, maar dat het water heel snel stijgt in het begin en steeds langzamer gaat stijgen. Maar tot nu toe hebben leerlingen enkel nog “uit het hoofd” deze situatie onderzocht en de modellen zijn daarom ook niet nauwkeurig. We willen dat de leerlingen hun eigen modellen gaan evalueren met behulp van de computersimulatie van het vullen van het cocktailglas op vergelijkbare wijze als ze dat klassikaal hebben gedaan. We ondersteunen de leerlingen om te letten op kwalitatieve aspecten van de modellen. Daarna gaan ze een nieuw model maken op basis van de simulatie.

in tweetallen | in groepjes

Tot nu toe hebben jullie tekeningen gemaakt van de stijgsnelheid door te bedenken hoe het water stijgt in het cocktailglas. Jullie gaan nu onderzoeken in hoeverre jullie tekening overeenkomt met hoe het water echt stijgt. We doen dat met behulp van een computersimulatie. Probeer maar uit!

  • Schrijf jullie namen op het antwoordvel.

  • Beantwoord de volgende vragen:

    1. Wat gebeurt er met de stijgsnelheid tijdens het vullen van het cocktailglas?
    2. Klopt jullie tekening met wat jullie zien? Waarom wel / niet?
    3. Stijgt het water overal even snel? Waarom wel/niet?
    4. Wanneer stijgt het water het snelst en waarom?
    5. Wanneer stijgt het water het langzaamst en waarom?
    6. Wat gebeurt er met de tijd en de hoogte?

in tweetallen | in groepjes

  • Schrijf jullie namen op het antwoordvel.

  • Maak met behulp van de computersimulatie een nieuwe tekening van de stijgsnelheid van het cocktailglas.

    • Probeer de tijd en de waterhoogte op te nemen in de tekening
    • Probeer in de tekening ook uit te leggen waarom het water langzamer stijgt als het glas breder is en sneller stijgt als het glas smaller is.

  • Zorg ervoor dat jullie allemaal tevreden zijn met de tekening en aan de hand ervan kunnen uitleggen wat de stijgsnelheid is.

  • In de volgende activiteit presenteren sommige leerlingen hun tekening voor de klas.

Bij het beantwoorden van de deelvragen zullen de leerlingen regelmatig de relatie tussen vorm en stijgsnelheid benoemen. Om te voorkomen dat het een betekenisloos mantra wordt, moeten de leerlingen het waarom achter die relatie uitdiepen. Dit is moeilijk onder woorden te brengen of te tekenen, maar juist dat proberen, zowel in groepsverband als klassikaal, ondersteunt de leerlingen in het modelleren.

Sommige leerlingen zullen teruggrijpen op eerdere modellen en die verfijnen. Andere leerlingen zullen bestaande modellen verwerpen en een nieuw soort model gaan uitproberen. Zo tekenden Roel en Maria een grafiek (zie Figuur 5):

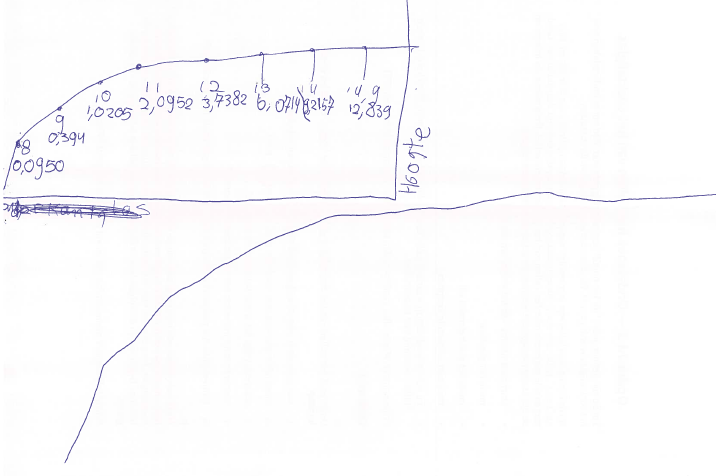
De grafiek van Maria en Roel

Maar let op! Op het eerste gezicht lijkt het een normale grafiek, maar de afstand tussen de punten en de bijgeschreven waarden komen niet overeen. Het lijkt erop dat de horizontale afstand tussen punten overeenkomt met stapgrootten van 1 cm, maar de verticale as hebben de leerlingen aangeduid als hoogte. De stapgrootten van de horizontale as komen niet overeen met de verschillen in tijd. Het meest voor de hand liggend is dat het verschil tussen de y-waarden van de punten een indicatie van de stijgsnelheid is en dat de afstand tussen de punten, die steeds even groot is, de stappen of intervallen aangeeft. Niettemin komt de vorm van de lijn overeen met die van een hoogte/tijd-grafiek.

Leerlingen kunnen modellen maken die ons als meer ervaren modelgebruikers vertrouwd overkomt, maar de leerlingen hebben niet onze achtergrond waarmee we betekenis geven aan dergelijke standaardmodellen.

4.2.5 Meer kwantitatieve modellen van de stijgsnelheid

Inventariseer en bespreek de verschillende modellen.

  • Laat per soort model een groep hun model presenteren

  • Evalueer het model met de klas:

    • Welk aspect wordt “beter” gemodelleerd? Waarom?
    • Welk aspect wordt niet of minder “goed” gemodelleerd? Waarom?

    Zorg ervoor dat leerlingen hun kritiek onderbouwen met argumenten.

  • Ga dieper in op de kwantitatieve aspecten van het model:

    • kan het model gebruikt worden om op een tijdstip de hoogte te bepalen?
    • of andersom (tijd bepalen gegeven de hoogte)?
    • hoe zou het model aangepast kunnen worden om dit te verbeteren?
    • hoe snel stijgt het water eigenlijk?

De leerlingen hebben ondertussen een beter idee ontwikkeld wat een goed model is, maar hebben enkel het cocktailglas gemodelleerd. Een aspect van modelleren is het kunnen toepassen van een model in andere, maar vergelijkbare situaties. Geef de leerlingen een ander glas, zoals een cognacglas of een wijnglas en vraag ze om daar een model van te maken.

De helft van de klas krijgt een wijnglas en de andere helft een cognacglas.

tweetallen | in groepjes

  • Schrijf jullie namen op het antwoordvel

  • Bekijk het glas en gebruik de simulatie

  • Maak samen een tekening van de stijgsnelheid in dit glas. Zorg ervoor dat jullie aan andere leerlingen kunnen uitleggen wat de stijgsnelheid is.

We verwachten dat de leerlingen heel wel in staat zijn om hun model aan te passen aan de nieuwe situatie, maar dat het niet vanzelf gaat. Leerlingen lopen tegen problemen aan omdat de situaties verschillen, maar ze lossen die problemen ook zelf op of ze benoemen de problemen.

Teken klassikaal een model van het wijnglas en een van het cocktailglas. Bespreek de modellen. Wat zijn de overeenkomsten, wat zijn de verschillen. Zouden de leerlingen aan kunnen geven hoe je van een willekeurig glas een tekening van de stijgsnelheid maakt?

Problematiseren van momentane stijgsnelheid:

Wat is die stijgsnelheid eigenlijk?

Kunnen we die meten? Hoe? Wat voor maat zouden we er voor gebruiken?

(dit moet nog verder uitgewerkt)

4.3 De momentane stijgsnelheid en de grafiek

De les begint, voortbouwend op de modellen van de leerlingen uit de vorige les, met de introductie van de grafiek als een model voor de stijgsnelheid in het cocktailglas. De leerlingen relateren de grafiek aan hun modellen uit de vorige les en kunnen sterke en zwakke punten van de grafiek aanwijzen in vergelijking tot hun eigen modellen.

De leerlingen zijn in staat om de grafiek te interpreteren en punten af te lezen. Daarnaast herkennen ze het patroon van verandering van het waterpeil in het cocktailglas.

De leerlingen realiseren zich dat hoe steiler de lijn stijgt, hoe sneller het water stijgt in het cocktail glas. Ze leggen de relatie tussen breedte van het glas, de steilheid van de lijn en de stijgsnelheid. Gegeven hun ontwikkelende begrip van deze situatie is het hen op zich niet vreemd dat de grafiek een vloeiende kromme is, ondanks dat ze grafieken eigenlijk alleen kennen als rechte lijnen of lijnstukken. Tegelijkertijd zijn ze niet in staat om uit te leggen waarom de lijn een vloeiende kromme is en wat dat betekent voor de stijgsnelheid en vice versa. Deze les gaat over dit probleem.

Deze kromme lijn past bij hun kwalitatief begrip van de veranderende snelheid in het cocktail glas van heel snel in het begin tot heel langzaam op het einde. Omdat de steilheid van de lijn juist op deze punten het meest extreem is en het meest verschilt, leggen de leerlingen de relatie tussen de steilheid van de lijn en de stijgsnelheid op dat moment.

We vragen de leerlingen of en hoe ze zouden kunnen bepalen hoe snel het water stijgt op een bepaald tijdstip of hoogte. We verwachten dat ze deze vraag niet kunnen beantwoorden. Tot nu toe hebben ze enkel kwantitatief over de situatie gedacht in termen van hoogtestijging en later ook gecoördineerd met de bijbehorende verstreken tijd. Het kwantificeren van de stijgsnelheid in relatie tot de steilheid van de lijn is het onderwerp van deze les.

4.3.1 Evalueer de grafiek als model voor de stijgsnelheid

Introductie van de grafiek van het cocktailglas als standaardmodel:

  • Kennen de leerlingen dit soort tekeningen? Waar worden ze voor gebruikt?
  • Wat valt de leerlingen op

in groepjes

  • Schrijf jullie namen op het antwoordvel.

  • Bespreek de grafiek als tekening voor de stijgsnelheid van het cocktailglas en beantwoord de volgende vragen:

    • Wat zijn de sterke punten?
    • Wat zijn de zwakke punten?
    • Vergelijk met jullie vorige tekeningen.
      • Wat kun je met de grafiek beter uitleggen dan met die tekening
      • Wat kon je met die tekening beter uitleggen dan met de grafiek?
    • Hoe komt de stijgsnelheid naar voren in de grafiek?
    • Waarom zouden we deze grafiek gaan gebruiken?

Bespreek de evaluaties van de grafiek:

  • Waarom zouden we deze grafiek gaan gebruiken?
  • Waarom is de grafiek een kromme lijn?
  • Hoe komt de stijgsnelheid naar voren in de grafiek?
    • Waar stijgt het water het snelst?
    • Waar het langzaamst en hoe zie je dat aan de grafiek (de leerlingen weten het antwoord immers al)

De leerlingen konden de grafiek interpreteren door het aflezen van punten paartjes (hoogte, tijd). B

We verwachten dat leerlingen tijdens de discussie over de stijgsnelheid in de grafiek vooral verwijzen naar de hoogte van het water, maar niet kunnen verwoorden wat de stijgsnelheid nu precies is. De leerlingen bekijken verschillende hoogten in isolatie zonder ook de tijd te coördineren. We verwachten dat leerlingen moeite hebben om in te zoomen op wat er verandert en hoe dat verandert.

We denken dat we de leerlingen deze horde kunnen laten nemen door middel van een staafjesgrafiek. Door leerlingen op het verschil tussen de hoogten van de staafjes te wijzen (zoals in Figuur 6) wordt het hen duidelijk dat het verschil tussen staafje aan het begin van de grafiek een stuk hoger is dan aan het einde. Dit verschil heeft blijkbaar te maken met de steilheid van de lijn en de stijgsnelheid.

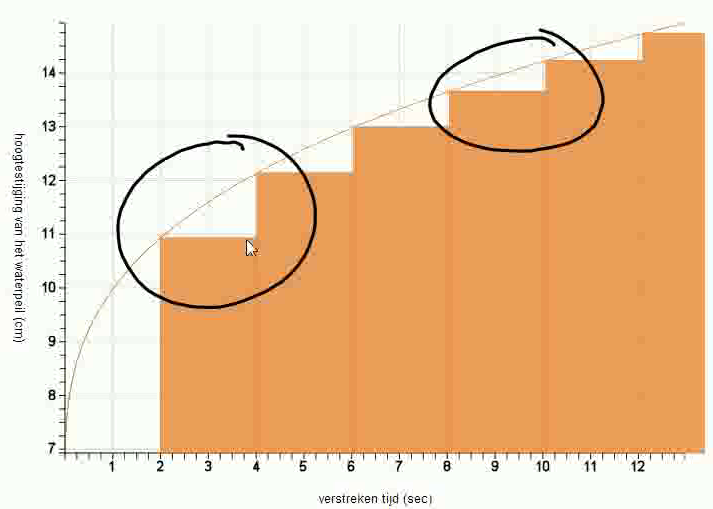
Vergelijk de staafjes: wat is het verschil tussen de eerste twee staafjes en de laatste twee staafjes?

Tijdens ons vorige experiment ervoeren we dat leerlingen en docent/onderzoeker onzorgvuldig met (wiskundige) taal omgaan en dat daardoor verwarring ontstaat. De termen schuin, steil, recht (horizontaal en verticaal recht) werden gebruikt om de steilheid van de lijn en de bijbehorende stijgsnelheid aan te duiden. Het is belangrijk tijdens de lessen duidelijk en consistent met taal om te gaan en, waar nodig, termen te introduceren of af te spreken.

4.3.2 De grafiek van het longdrinkglas

We gaan de steilheid van een lijn onderzoeken met behulp van longdrinkglazen. Het vullen van een longdrinkglas is een lineaire situatie waarin de stijgsnelheid constant is. Hierdoor is de grafiek altijd een rechte lijn. Hoe steiler de lijn, hoe sneller het water stijgt. We verwachten dat leerlingen, al dan niet met ondersteuning, in staat zijn om de stijgsnelheid van het longdrinkglas uit te rekenen aan de hand van de grafiek. Hierbij wordt we het idee van een “snelheidsdriehoek” (zie Figuur 7) om die snelheid uit te rekenen geïntroduceerd.

verstreken tijd gestegen hoogte steilheid, snelheid = gestegen hoogte verstreken tijd
De snelheidsdriehoek: de steilheid, de snelheid = gestegen hoogte / verstreken tijd

We geven de leerlingen een longdrink glas in handen en vragen hen wat er gebeurt bij het vullen van het glas. Vervolgens vragen we hen om de grafiek van het longdrinkglas te schetsen zonder gebruik te maken van de computer.

in groepjes

  • Schrijf jullie namen op het antwoordvel.
  • Jullie zien hier een longdrinkglas. Zonder de computer te gebruiken, schets de grafiek van het longdrinkglas
  • Beredeneer waarom de grafiek er zo uit zal zien

Omdat leerlingen een goed begrip hebben ontwikkeld van de relatie tussen de breedte van een glas en de stijgsnelheid begrijpen ze dat in deze situatie de stijgsnelheid niet verandert en dus “steeds hetzelfde is”. Een grafiek hiervan tekenen is minder eenvoudig dan het lijkt, de leerlingen hebben weinig ervaring met het tekenen van een grafiek, maar we verwachten dat leerlingen deze situatie met een rechte lijn modelleren. De leerlingen koppelen deze rechte lijn aan het constant zijn van de stijgsnelheid en de vorm van het glas.

in groepjes

Controleer jullie grafiek met behulp van de computer:

  • Klopte jullie grafiek?

  • Waarom is de grafiek een rechte schuine lijn?

  • Kunnen jullie een manier bedenken om de stijgsnelheid van het longdrinkglas te berekenen?

We vragen leerlingen of en hoe ze in deze situatie de stijgsnelheid van het water in het glas kunnen bepalen op een bepaald tijdstip. Omdat de snelheid overal hetzelfde is, is het gelijk aan de gemiddelde snelheid en dus ook gelijk aan de totale stijging gedeeld door de tijd die daarvoor nodig was. Deze snelheid past bij het begrip van snelheid waarmee de leerlingen bekend zijn als een verhouding van afgelegde weg (in dit geval de stijging van het waterpeil) en een periode uitgedrukt in een bekende eenheid zoals cm/sec. Maar we verwachten niet dat alle leerlingen deze link tussen gewone snelheid en stijgsnelheid zelfstandig leggen. Daarbovenop verwachten we niet dat leerlingen hun bestaande kennis van het berekenen van snelheid toe kunnen passen in deze nieuwe situatie zonder ondersteuning.

Merk op dat zelfs als leerlingen de standaardformule aan kunnen passen en uitvoeren dit geen uiting van dieper begrip van snelheid hoeft te zijn, maar ook een vorm van numeriek/algoritmisch begrip zonder bijbehorend wiskundig begrip. Leerlingen geven blijk snelheid kwalitatief te begrijpen en kunnen numerieke procedures toepassen, maar we kunnen er niet van uitgaan dat ze hun kwantitatief begrip van snelheid tot een vergelijkbaar niveau hebben ontwikkeld. Uitingen van numerieke vaardigheid zijn dan ook geen uitingen van kwantitatief begrip. Om dat kwantitatieve begrip te ontwikkelen is meer nodig dan het verwijzen naar en toepassen van numerieke procedures.

  • Bespreek de grafiek van het longdrinkglas en de voorgestelde manieren om de stijgsnelheid te bepalen.

  • Leg de relatie met het berekenen van gewone snelheid.

    • Wat is snelheid eigenlijk?
    • Hoe berekenen we snelheid?
    • Wat is de gebruikelijke eenheid en wat betekent die (in relatie tot snelheid?)

  • Bereken de stijgsnelheid met behulp van de snelheidsdriehoek

  • Bespreek de relatie tussen deze berekening, de stijgsnelheid en de steilheid van de grafiek.

We verwachten dat deze discussie de voorkennis van de leerlingen aanspreekt en hen in staat stelt om hun begrip van de stijgsnelheid meer kwantitatief te ontwikkelen om daarmee begrip van momentane snelheid te ontwikkelen.

4.3.3 De grafiek van het longdrinkglas als maat voor de momentane snelheid

Bespreek de relatie tussen de steilheid van een grafiek van een longdrinkglas en de grafiek van het cocktailglas.

We laten de leerlingen het cocktailglas en het longdrink glas zien en vragen hen wanneer het water even snel stijgt in het cocktail glas als in het longdrink glas. De leerlingen hebben een goed begrip van de relatie tussen breedte van het glas en de stijgsnelheid en beseffen dat als de twee glazen even breed zijn, dat dan het water even snel stijgt. De leerlingen beseffen, al dan niet na er op gewezen te zijn, dat ze de snelheid op dat moment nu weten.

We vragen de leerlingen hoe ze de snelheid op een ander moment zouden kunnen bepalen. Ze begrijpen dat ze hiervoor een ander longdrink glas kunnen gebruiken dat even breed is als het cocktail glas op dat moment. De computersimulatie stelt de leerlingen in staat om zo’n longdrink glas te maken, de grafiek ervan te tekenen en met behulp daarvan de stijgsnelheid te bepalen. Dit is echter een complexe handeling en we verwachten dat de leerlingen hierbij enige ondersteuning nodig hebben.

We vragen de leerlingen hoe ze aan de grafieken van de longdrink glazen en het cocktail glas kunnen zien dat het water op dat moment met dezelfde snelheid stijgt. Doordat leerlingen de relatie tussen stijgsnelheid en steilheid van de lijn hebben gelegd, en twee verschillende schuine lijnen hebben gezien voor de twee verschillende longdrink glazen, ligt het voor de hand dat ze zich focussen op de steilheid van deze rechte lijnen. We verwachten niet dat de leerlingen de steilheid koppelen aan een punt op de kromme van het cocktail glas zonder dat ze daarbij ondersteund worden, bijvoorbeeld door de rechte lijnen op die punten op de kromme te tekenen. Dan wordt expliciet de relatie gelegd tussen deze raaklijnen en de steilheid van de kromme.

We vragen de leerlingen of en hoe ze enkel met behulp van de grafiek de stijgsnelheid op een bepaald punt zouden kunnen bepalen. De leerlingen zullen aangeven dat ze door “zo’n lijntje” of “driehoek” te tekenen de snelheid kunnen bepalen, maar heel veel verschillende raaklijntjes benaderen zo op het oog de steilheid van een kromme. Welk raaklijntje is de beste / juiste? Maakt het veel uit voor het uitrekenen van de stijgsnelheid? Leerlingen weten dat dit te maken heeft met het bij de raaklijn horende longdrink glas en de breedte van het cocktail glas op dat moment. Tegelijkertijd ontdekken ze dat veel andere lijntjes de stijgsnelheid vrij goed benaderen omdat de stijgsnelheid die ze ermee uitrekenen niet veel verschilt. We hopen dat leerlingen hierdoor de raaklijn gaan zien als een geschikte maat en middel om de stijgsnelheid te bepalen. We introduceren de snelheidsdriehoektool die automatisch een geschikte snelheidsdriehoek tekent op een punt van een kromme.

4.3.4 Momentane snelheid in het cocktailglas

in tweetallen

  • Schrijf jullie namen op het antwoordvel.

  • Er zijn drie verschillende longdrinkglazen. Bepaal de stijgsnelheid van elk van deze longdrinkglazen.

    Jullie mogen een rekenmachine gebruiken

    1. longdrinkglas A
    2. longdrinkglas B
    3. longdrinkglas C

  • Bepaal het tijdstip waarop het water in het cocktailglas even snel stijgt als in de drie longdrinkglazen

    1. moment voor longdrinkglas A
    2. moment voor longdrinkglas B
    3. moment voor longdrinkglas C

    Beredeneer en laat zien waarom jullie antwoord klopt.

In het vorige experiment hadden leerlingen moeite met het bepalen van de stijgsnelheid. De leerlingen wilden de stijgsnelheid uit te rekenen door dezelfde manier toe te passen als bij het longdrinkglas en ze bepaalden de gemiddelde stijgsnelheid op het interval 0 tot 6 seconden (2 cm/sec). Vervolgens vroeg ik de leerlingen hoe de grafiek er uit zou zien van een longdrinkglas waarin het water met 2 cm/sec stijgt. De leerlingen tekenden vervolgens de een lijn vanuit de oorsprong naar het punt (6, 12.5) (zie Figuur 11).

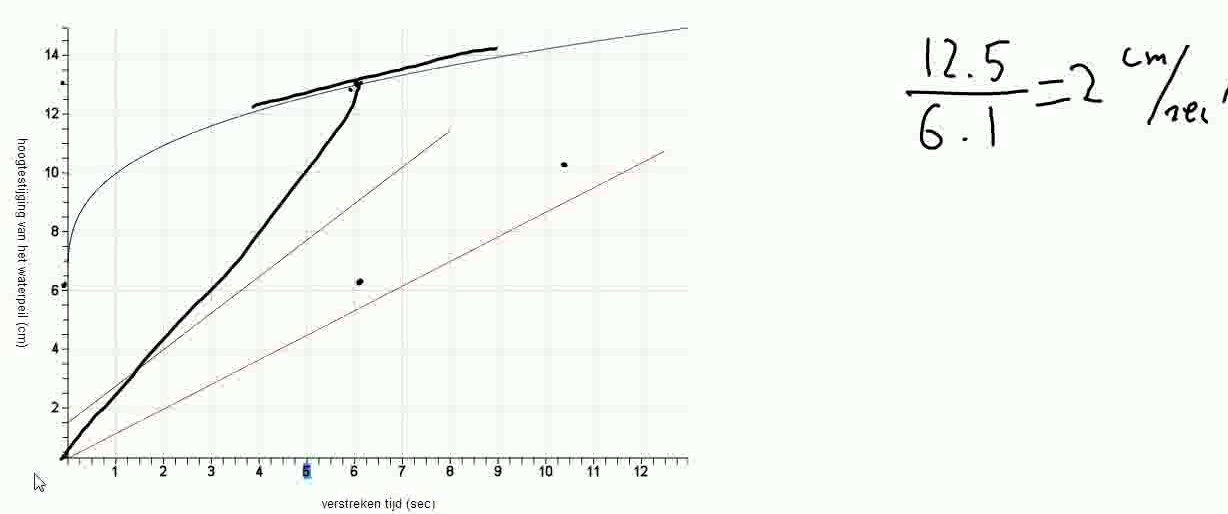
Gemiddelde snelheid ≠ momentane snelheid

De volgende discussie vond vervolgens plaats:

Huub In, inderdaad, dus het is gewoon een rechte lijn van 0 naar 12 en van 0 naar 6. Dat hebben we uitgerekend.

Nou hebben we een aantal keer geleden, hebben we bij de vorige les gezegd dat ehm de stijgsnelheid heeft te maken met de steilheid of de schuinheid van de lijn. Nou is mijn vraag aan jullie: is de schuinheid van deze rechte lijn hetzelfde als de schuinheid van de grafiek op dat punt (wijst naar de grafiek van het cocktailglas bij 6 seconden)?

Maria Hmm, ik denk het wel

Huub Dus, als ik hier een lijn zou tekenen (tekent een raaklijn aan de grafiek van het cocktailglas bij 6 seconden. Zie ook Figuur 11). Ja, hij loopt ongeveer zo schuin, dan is deze lijn en die lijn even schuin?

Maria Nee

Huub Nee, dat is vreemd

Maria Alleen, alleen dit puntje (loopt naar het bord en wijst het punt bij 6 seconden aan). Zo

Huub Alleen dat puntje?

Maria Als je, zeg maar, deze zou draaien (probeert het raaklijntje te draaien, computer ‘slaat op hol’)

Huub Kunnen, kunnen we niet, die wil je draaien, hier heb je een lijn, die wil je draaien. Hoe wil je die dan draaien?

Maria Ja, zo

Huub Dat ie er zo uitziet (tekent een lijn parallel met het rechte lijntje). Maar dan is het niet de zelfde schuinheid meer

Maria Nee, maar ik bedoel, alleen (loopt naar het bord)

Huub Raak het scherm maar niet aan, ja

Maria Alleen dit puntje, zeg maar, ik weet niet, eigenlijk dat alleen

Huub Dus je wilt alleen maar dit puntje hebben (tekent het puntje op de grafiek)

Maria Ja

Huub Maar dan is eigenlijk de vraag: hoe schuin is de lijn op dat puntje?

Maria Eeuh, het kan alle kanten, ja

Vervolgens verschoven we onze aandacht naar de lijn van het longdrinkglas (bruine lijntje) en de leerlingen gaven aan waar de grafiek van het cocktailglas even schuin liep (zie ook Figuur 12)

Leerlingen geven aan waar de rechte lijn en de kromme gelijk lopen

Huub Dus van die rechte lijn is dan inderdaad de snelheid 2 cm/sec. Maar wat is nu de stijgsnelheid van het cocktailglas?

En als ik jullie vraag wanneer het water even snel stijgt in het cocktailglas als in deze bruine lijn? Wat zouden jullie dan gaan gokken, of kiezen, of

Roel (staat op en loopt naar het bord) Ik zou dat dan ongeveer hier en daar (wijst een punt aan op de bruine rechte lijn en op de lijn van het cocktailglas)

Huub Oké, waarom daar?

Roel Ja, hier (wijst op de bruine rechte lijn) maakt het niet veel uit, maar hier ongeveer zo (beweegt met zijn hand een rechte lijn rakend aan dat van het cocktailglas, min of meer parallel aan de bruine lijn)

Huub Kun je dat tekenen?

Roel (tekent) Dit stukje is ongeveer, zo ongeveer (tekent een kort lijnstukje op de bruine lijn en de lijn van het cocktailglas)

Huub Oké.

En wat is dan hetzelfde. Is deze bruine lijn en dit zwarte lijntje

Roel Dan stijgt ie even snel (maakt met twee handen parallel een beweging van linksonder naar rechtsboven), dan staan de lijntjes staan dezelfde kant op

Huub Oké, ze staan dezelfde kant op, wat houdt dat in voor de schuinheid van die twee lijnen

Bepaal de stijgsnelheid met een driehoek

Uit dit vignet blijkt dat leerlingen inderdaad De leerlingen begrepen dat als een longdrinkglas even breed is als het cocktailglas dat dan, op dat punt, het water even snel stijgt. De leerlingen begrepen dat als de grafiek van het cocktailglas even steil liep als dat van een longdrinkglas dat daar, op dat punt het water even snel stijgt. De leerlingen konden, met enige ondersteuning, de numerieke procedure uitvoeren om een stijgsnelheid te berekenen van de grafiek van een longdrinkglas. Hierbij was een “verschildriehoek” een handig hulpmiddel. De leerlingen hadden echter geen kwantitatief begrip ontwikkeld van een (momentane) snelheid en de idee van een momentane snelheid bleef wat op de achtergrond.

Leerlingen zijn in staat om de steilheid van een lijn te koppelen aan de snelheid. Ze kunnen beoordelen of het water op een punt sneller of langzamer stijgt. Die snelheid betekenisvol kwantificeren, daarentegen, blijkt lastiger. Leerlingen verwarren een punt (notabene de hoogte), de gemiddelde snelheid tot dat punt en de momentane snelheid op dat punt. Ze “meten” en goochelen vervolgens met die getallen en voeren berekeningen uit, ogenschijnlijk zonder te weten wat ze doen. Het ligt voor de hand leerlingen het verschil tussen een punt, de gemiddelde snelheid en de momentane snelheid expliciet te laten maken, te laten onderzoeken en te laten modelleren.

  • Bespreek de door de leerlingen berekende stijgsnelheden en bijbehorende momenten.
  • Bespreek momentane snelheid:
    • Wat is eigenlijk een momentane snelheid
    • Gebruik als voorbeeld het wijnglas of het cognacglas: hoe snel stijgt het water op t=X seconden?

We verwachten dat veel leerlingen zullen verwijzen naar de procedure om die momentane snelheid te bepalen als verklaring van een momentane snelheid. Maar dat is geen uitleg wat een momentane snelheid is.

Eventuele extra opdrachten:

5 Intermezzo

Na de lessen over stijgsnelheid bij het vullen van glazen, reflecteren we op het leerproces van de leerlingen. Op basis van deze reflectie zetten we het volgende deel van de lessenserie op. We letten met name op:

Vervolgens werken we Deel B in meer detail uit omdat we nu beter kunnen voorspellen wat we van de leerlingen kunnen verwachten en hoe we hun leerproces kunnen leiden naar verder verdieping van het begrip van momentane snelheid.

6 Deel B: Effecten van isolatiemateriaal op afkoelings- en opwarmingssnelheid

De voorspellingen en verwachtingen van het begrip en begripsontwikkeling van de leerlingen in dit deel moet nog uitgewerkt worden. Ik heb dit onderdeel nog niet eerder uitgeprobeerd, dus deze voorspellingen en verwachtingen zullen gedurende de uitvoering van deel A verder uitkristalliseren. In het Intermezzo finetunen we deze verwachtingen.

6.1 Inleiding — Onderzoeksopdracht

Het doel van Deel B is om te onderzoeken hoe en in hoeverre het begrip van de leerlingen van momentane stijgsnelheid de overstap maakt naar en andere context en hoe die overstap ondersteund kan worden. We willen dat leerlingen na Deel B een meer algemeen begrip van momentane snelheid hebben ontwikkeld dat ze flexibel in kunnen zetten bij het onderzoeken van dynamische systemen en het interpreteren van lijngrafieken.

In de lessen van dit deel onderzoeken de leerlingen de afkoelings- en opwarmingssnelheid van water en het effect van isolatiematerialen op die snelheid. In de introductieles over afkoeling en opwarming gaan de leerlingen op basis van hun huidige begrip van de situatie en snelheid een voorspelling doen over de opwarming en afkoeling van water. Vervolgens relateren ze die voorspelling aan een door de computer gemeten afkoeling en opwarming. We gaan op zoek naar hoe de snelheid verandert gedurende de afkoeling of opwarming en proberen te beredeneren hoe.

In de tweede les gaan de leerlingen onderzoeken wat het effect is van verschillende isolatiematerialen op die snelheid. Elke groep onderzoekt een materiaal door een voorspelling te doen, die te controleren, en proberen te verklaren hoe het isolatiemateriaal werkt. Hierna worden deze resulaten in de klas gepresenteerd en bijeengeraapt om te bepalen welk isolatiemateriaal het beste is. De leerlingen bedenken een manier om de verschillende materialen overzichtelijk weer te geven en te vergelijken en schrijven een kort rapportje over het onderzoek, de resultaten en wat er bij komt kijken.

6.2 Benodigdheden

6.3 Afkoeling van een kop thee / opwarming van ijswater

Introduceer het afkoelen van een kop thee als een onderzoekssituatie:

  • Wat gebeurt er met de temperatuur van een kop warme thee?
  • Wat kunnen jullie zeggen over de afkoelingssnelheid?
  • Hoe kunnen we die afkoelingssnelheid / temperatuur bepalen?

Introduceer het meten van de temperatuur met behulp van de computer en een sensor. Deze sensor doet precies hetzelfde als een leerling zou doen, namelijk de temperatuur op een moment opmeten en opschrijven, maar dan automatisch elke zoveel milliseconden.

Start het meetproces. De leerlingen kunnen de resultaten later gebruiken om hun eerste ideeën te staven.

in groepjes

  • Voorspel wat er gebeurt met de afkoelingssnelheid van een kop warme thee.
  • Schets een grafiek van de afkoelingssnelheid.
  • Beredeneer / leg uit waarom jullie voor deze grafiek kiezen

  • Laat een aantal groepen hun grafiek presenteren en uitleggen. Bespreek de verschillende grafieken en de afkoelingssnelheid van het theewater.

  • Laat de ondertussen gemeten afkoelingsgrafiek zien. Bespreek de verschillen met de grafieken van de leerlingen.

  • Onderzoek de afkoelingssnelheid:

    • Wanneer koelt het water het snelst af, wanneer het langzaamst
    • Waarom?
    • Hoe snel koelt het water af?

  • Onderzoeksvraag: wat gebeurt er met de opwarmingssnelheid van een bekertje ijswater? Zet weer de sensor aan.

in groepjes

  • Voorspel wat er gebeurt met de opwarmingssnelheid van het ijswater.
  • Teken een grafiek van de opwarmingssnelheid.
  • Leg uit waarom het water zo opwarmt.

  • Bespreek aan de hand van de gemeten opwarmingsgrafiek de opwarming van water

  • Wat gebeurt er met de opwarmingssnelheid en waarom?

  • Is er een manier om die opwarmingssnelheid of afkoelingssnelheid te vertragen?

    • Bedenk verschillende manieren (thermofles, ijskast, isolatie, …)
    • Bedenk manieren om te onderzoeken welke manier het beste werkt

6.4 Isolatiemateriaal en afkoelingssnelheid

Terugkoppelend op de vorige les: hoe kunnen we onderzoeken op welke manier we het best de afkoelingssnelheid of opwarmingssnelheid kunnen vertragen.

Bespreek de onderzoeksmethode en verdeel de verschillenende isolatiemanieren onder de groepjes om te onderzoeken.

We willen een duidelijk overzicht maken dat inzicht geeft in hoe de verschillende isolatiematerialen/manieren de opwarmingssnelheid/afkoelingssnelheid vertraagt zodat we ze gemakkelijk kunnen vergelijken en bespreken.

in groepjes

  • Onderzoek de vertraging van de afkoelingssnelheid/opwarmingssnelheid van een isolatiemateriaal/manier
  • Maak een voorspelling
  • Meet ondertussen met de sensor
  • Vergelijk de voorspelling met de meetgrafiek
  • Geef een oordeel over dit isolatiemateriaal
  • Bereid een presentatie van jullie onderzoek en resultaten
  • Presenteer en inventariseer de resultaten van de verschillende isolatiematerialen
  • Welke is het best?
  • Hoe zouden we de resultaten overzichtelijk kunnen weergeven?

(Eventueel, afhankelijk van de overkoepelende context)

in groepjes

Schrijf een kort verslag over isolatiematerialen, onderzoek, grafieken, enzovoorts

6.4.1 Afronding

Afsluiting lessenserie:

  • Bedanken leerlingen en docent.
  • Evaluatie leerlingen.
  • Evaluatie begrip momentane snelheden, bijvoorbeeld in weer een andere context.

7 Bijlagen

7.1 Werkbladen

7.2 Handleidingen, discussieschema’s en evaluatieschema’s

7.3 Website en software

De software die we tijdens de lessenserie gebruiken, is toegankelijk via: http://primarycalculus.org/DOEN/.

OPMERKING: op dit moment bestaat deze URL nog niet, ik ben bezig met het verbeteren van de software uit het vorige experiment (zie http://primarycalculus.org/tue-experiment/les2.html)

De software bestaat uit vier componenten:

  1. een simulatie van het vullen van glazen
  2. een grafiekcomponent waarin grafieken van het dynamische systeem dat de leerlingen onderzoeken getekend worden.
  3. een tabel waarin de veranderlijke grootheden van het dynamische systeem worden weergegeven en het systeem “uitgevoerd” kan worden.
  4. een sensorcomponent waarmee de temperatuursensor wordt uitgelezen.

In Figuur (hieronder) zie je de simulatie, tabel en grafiekcomponenten uit het vorige experiment.

Software gebruikt tijdens het vorige experiment: een simulatie, tabel en grafiek

De nieuwe versie kent een aantal functionele verbeteringen en ook het uiterlijk zal verbeterd worden, met name:

Daarnaast ben ik nog bezig met het nadenken over hoe de docent (en onderzoeker) het beste toegang kan krijgen tot het digitale werk van de leerlingen, bijvoorbeeld voor gebruik tijdens klassediscussies. Daarnaast wil ik voor het onderzoek toegang tot deze gegevens om ze achteraf te kunnen analyseren.

Literatuur

Ainley, J., Pratt, D., & Nardi, E. (2001). Normalising: children’s activity to construct meanings for trend. Educational Studies in Mathematics, 45(1), 131–146.
Bock, D. de, Dooren, W. van, Janssens, D., & Verschaffel, L. (2002). Improper use of linear reasoning: An in-depth study of the nature and the irresistibility of secondary school students’ errors. Educational Studies in Mathematics, 50(3), 311–334.
Buijs, K., Klep, J., & Noteboom, A. (2008). TULE - Rekenen/wiskunde. Inhouden en activiteiten bij de kerndoelen. Inhoud van de website tule.slo.nl. Retrieved from http://www.slo.nl/downloads/2008/tule-rekenenwiskunde2011.pdf
Coll, R. K., France, B., & Taylor, I. (2005). The role of models and analogies in science education: implications from research. International Journal of Science Education, 27(2), 183–198. http://doi.org/10.1080/0950069042000276712
Coll, R. K., & Lajium, D. (2011). Modeling and the Future of Science Learning. In M. S. Khine & I. M. Saleh (Eds.), Models and Modeling (Vol. 6, pp. 3–21). Springer Netherlands.
Galen, F. van, & Gravemeijer, K. (2010). Dynamische grafieken op de basisschool. Ververs foundation. Retrieved from http://www.fi.uu.nl/rekenweb/grafiekenmaker/documents/dynamischegrafieken.pdf
Galen, F. van, Gravemeijer, K., Mulken, F. van, & Quant, E. (2012). Kinderen ononderzoeken ’snelheid’. Retrieved from http://www.fisme.science.uu.nl/rekenweb/grafiekenmaker/documents/kinderenonderzoekensnelheid.pdf
Gilbert, J. (2004). Models and modelling: Routes to more authentic science education. International Journal of Science and Mathematics Education, 2(2), 115–130.
Gilbert, J., & Boulter, C. (1998). Learning Science Through Models and Modelling. In B. J. Fraser & K. G. Tohin (Eds.), International handbook of science education (pp. 53–66).
Gilbert, S. (1991). Model building and a definition of science. Journal of Research in Science Teaching, 28(1), 73–79.
Kaput, J., & Schorr, R. (2007). Changing representational infrastructures chages most everything: the case of SimCalc, algebra and calculus. In G. Blume & K. Heid (Eds.), Research on technology in the learning and teaching of mathematics (pp. 211–253). Mahwah, NJ: Erlbaum. Retrieved from http://www.kaputcenter.umassd.edu/downloads/simcalc/cc1/library/changinginfrastruct.pdf
Lehrer, R., & Schauble, L. (2010). What Kind of Explanation is a Model? In M. K. Stein & L. Kucan (Eds.), Instructional explanations in the disciplines (pp. 9–22). Springer.
Louca, L. T., & Zacharia, Z. C. (2012). Modeling-based learning in science education: cognitive, metacognitive, social, material and epistemological contributions. Educational Review, 64(4), 471–492.
Schwarz, C. V., Reiser, B. J., Davis, E., Kenyon, L., Achér, A., Fortus, D., … Krajcik, J. (2009). Developing a learning progression for scientific modeling: Making scientific modeling accessible and meaningful for learners. Journal of Research in Science Teaching, 46(6), 632–654. http://doi.org/10.1002/tea.20311
SLO. (2006). Herziene kerndoelen basisonderwijs. Retrieved from http://www.slo.nl/primair/kerndoelen/Kerndoelen.doc/download
Stroup, W. (2002). Understanding qualitative calculus: A structural synthesis of learning research. International Journal of Computers for Mathematical Learning, 7(2), 167–215. Retrieved from http://www.springerlink.com/content/k211l7w34v628740/fulltext.pdf
Thompson, P. (1994). The development of the concept of speed and its relationship to concepts of rate. In G. Harel & J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 179–234). Albany: SUNY Press. Retrieved from http://pat-thompson.net/PDFversions/1994ConceptSpeedRate.pdf
Thompson, P., & Thompson, A. (1994). Talking about rates conceptually, part I: a teacher’s struggle. Journal for Research in Mathematics Education, 25(3), 279–303.
Yackel, E., & Cobb, P. (1996). Sociomathematical Norms, Argumentation, and Autonomy in Mathematics. Journal for Research in Mathematics Education, 27(4), 458–477. Retrieved from http://www.jstor.org/stable/749877