Translation
From Craftmanship to Science
Huub de Beer
August 2006
1 From craftsmanship to science
It is easy to point to ALGOL 60 and herald this language as the main stimulus for the emerging field of translator writing in computer science. Is this image of ALGOL 60 and the ALGOL effort as the catalyst to the development of the field of translator writing true? And if so, what part of the ALGOL effort was the most influential, and why?
In the 1960s ALGOL 60 was, especially in the academic world, an influential language. In the same period the field of translator writing was developing with big leaps. A chronological order, however, does not mean a causal order per sé. More importantly, the field of translator writing was not new. As mentioned before, there was already experience with the implementation of algebraic languages. This experience was, on the other hand, more practically oriented and lacked a sound theoretical fundament.
Most of these early efforts to create and implement algebraic languages were isolated efforts. Many different research groups and corporations were, independently of each other, creating their own languages. Publication of the results was rare, using each other’s work even more rare. Of course, there was communication between the different groups at symposia and conferences, for example. This contact, however, did not result in the development of a common theory of translation. The field of translator writing was a field of best practices and craftsmanship.
In the early 1960s, this situation would change drasticly. An article written by F.L. Bauer and K. Samelson, Sequential formula translation(Samelson & Bauer, 1960), about a translation technique used in their IAL translator was widely read and was often cited in subsequent articles on the translation of ALGOL 60 and translation of algebraic languages in general. It seemed that this article was the one sheep that was followed by many others.
One of the first to cite and use Bauer and Samelson’s article was E.W. Dijkstra in his 1960 article Recursive Programming(Dijkstra, 1960). In this article, Dijkstra presented a solution for the implementation of one of the most controversial features of ALGOL 60: recursive procedures. He had developed this solution while he was working, together with J.A. Zonneveld, on an ALGOL 60 translator for the Electrologica X1 at the Mathematical Centre in Amsterdam.
This translator was important because it was the first complete ALGOL
60 translator, only the use of the own concepts was somewhat
restricted.(Dijkstra,
1963a, p. 3) In August 1960, ten months after the start of the
project the translator was put into use.(Kruseman Aretz, 2003, p. 1) Only some
months after the publication of the ALGOL 60 report, Dijkstra and
Zonneveld proved that ALGOL 60 could be implemented in an efficient
way.
In 1961, Dijkstra published two articles on the making of this translator: An ALGOL 60 Translator for the X1(Dijkstra, 1963a) and Making a Translator for ALGOL 60(Dijkstra, 1963b). These article were also often cited and used by others. In these years, publication and referring to each other’s work became more and more the norm.
In 1962, the lack of a unifying theory in the field of translator writing would be solved by Ginsburg and Rice in Two Families of Languages Related to ALGOL(Ginsburg & Rice, 1962). In this article they connected a theory about different types of languages from theoretical linguistics with programming languages. From then on, formal languages became an intrinsic part of the field of translator writing. Eventually, theory, practice, experience, and research would lead to the development of powerful translation techniques and tools to do much of the work that, in the early 1960s, costed several man-years to complete.
In these years, the field of translator writing became a scientific field, and in this chapter, it is argued that the ALGOL effort was the catalyst to this transformation. To that end, the translation of algebraic expressions, in particular the technique pulished by Bauer and Samelson, is discussed first because it was the basis for both the language IAL and the development of many ALGOL translators.
Given this translation technique, basically three approaches to the translation of ALGOL 60 were taken: extending the technique, improving the technique, and, unrelated to the technique, developing other translation techniques. First, the approach of extending the technique is treated with the description of two articles about the implementation of procedures in ALGOL. With the treatment of procedures the most intriguing aspects of the ALGOL language are discussed: the procedure concept as such, recursion, call-by-value parameters, and call-by-name parameters.
The other two approaches towards the translation of ALGOL 60 are treated together because both were based on the structure of the definition of ALGOL 60 or the structure of the BNF. Some articles on the translation of ALGOL 60, published before 1962, are discussed in a more or less chronological order to give a good view of these approaches and the evolving field of translator writing.
Of course, after the publication of Two Families of Languages Related to ALGOL by Ginsburg and Rice (1962) there were many more developments in the field of translator writing. The focus in the field, however, shifted from translating ALGOL to translating ALGOL-like languages and even to the general problem of translation. Nonetheless, ALGOL 60 would often be the prime example or the first application of certain techniques and theories. And, long after 1962, ALGOL 60 translators were being build and improvements in techniques were being made. The field of translator writing stood on its own, free from the ALGOL effort and for the topic of this chapter, these later developments related to the translation of ALGOL are, though interesting, less relevant.
2 Sequential formula translation
During the 1950s, many algorithmic languages were invented and implemented. Eventually, a more general technique to translate algebraic formulae was developed independently by different people.(Knuth, 1972, p. 44) Due to the isolated nature of these early efforts and the lack of publications,(Knuth, 1972, p. 39) this technique was not widely known.
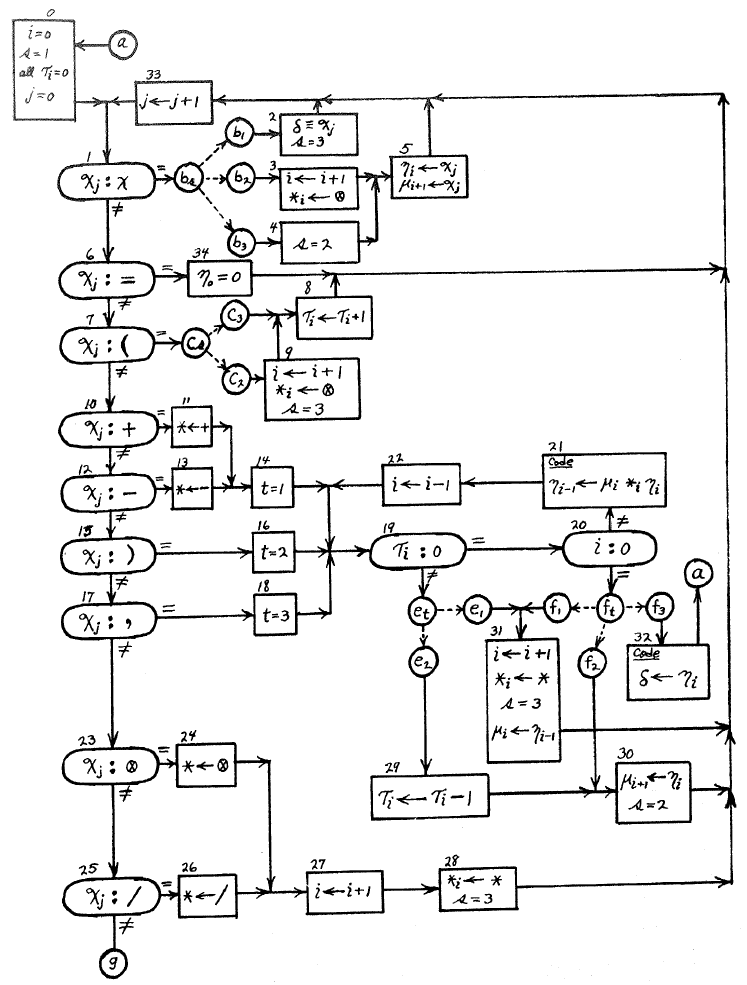
In March 1959, J.H. Wegstein was the first to publish this technique in a scientific journal. In From formulas to computer oriented language(Wegstein, 1959), Wegstein described the translation technique in less than three pages containing two tables and a huge flow-diagram (see above Figure). This article did not gain much attention, probably due to the date of publication.
Some months later, in November 1959, Bauer and Samelson published their version of the technique as iSequentielle Formelübersetzung(Friedrich L. Bauer & Samelson, 1959) in Elektronische Rechenanlagen, a new German scientific journal. Although this article was widely read in Europe, it would be the translated version published in early 1960 in the Communications of the ACM which became truly influential. Their Sequential formual translation(Samelson & Bauer, 1960) was referred to in almost all publications related to the translation of ALGOL and translation in general in the early 1960s.
As Bauer and Samelson were not the first to publish nor the only ones to develop this translation technique, the question arises: Why did their article and translation technique gain so much more attention and why was it so influential? Before answering this question, it must be said that only Bauer himself has written some historical papers about his and Samelson’s work on this translation technique and the developments leading to the publication of it. Unfortunately, no one else has written about Bauer and Samelson’s work nor about any of the other people developing a similar technique. Nonetheless, Bauer’s historical publications on this translation technique are, if used with care, an opportunity to describe the development of this technique in more detail.
2.1 The development of the sequential formula translation technique
Based on their early work on the STANISLAUS, a device to check a valuation of a propositional formula, Bauer and Samelson started in 1955 on a technique to translate arithmetic formulae.(F. L. Bauer, 1990, p. 43) They worked this technique into a design for a simple calculator (See Figure below) (Samelson & Bauer, 1962, pp. 207, 217), as we will now describe.
Formulae can be entered into the calculator using a keyboard. Numbers and operators are separated. The former go directly into the number stack (Numbers Cellar). Incoming operators are compared to the topmost operator on the operator stack (Operations Cellar) using the precedence orders in the Table below(Samelson & Bauer, 1962, p. 208): If the order of the incoming operator is lower than the order of the operator on the stack then the new operator is pushed onto the stack; If the orders are equal, the incoming operator is evaluated by the computer; If the order of the incoming symbol is greater than the operator on the stack, the latter is evaluated by the computer.
| order | incoming operator | topmost operator |
|---|---|---|
| 0 | \((\) | |
| 1 | \(\times, \div\) | \(\times, \div\) |
| 2 | \(+, -\) | \(+, -\) |
| 3 | \()\) | \((\) |
The computer component performs the evaluation of an operator using the topmost numbers on the number stack and the result is pushed back onto the number stack. When the end of an expression is reached, the result of the evaluation of the expression is available as the topmost element of the number stack and can then be printed.
As an example, the evaluation of the expression \((3 + 5) \times (-2 + 4)\) is described below. Initially, the number stack contains a \(0\) for the purpose of computing the unary operators \(+\) and \(-\). If the number stack becomes empty during a computation, the number \(0\) is again pushed onto the stack for the same reason. The evaluation of the expression is performed sequentially, that is, like “how the expression is read”, thus from left to right. The state of the calculator is given by the contents of the number stack, the operator stack and the current input symbol. The symbol \(\bot\) denotes the end of the stack.
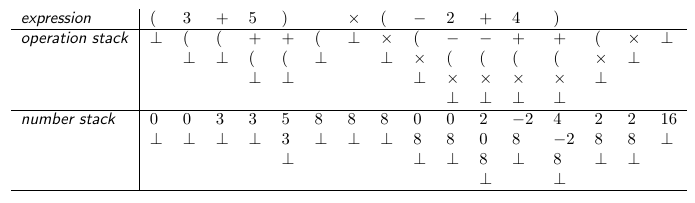
In 1956, Bauer, Bottenbruch, Rutishauser, and Samelson started a joint project to create an algebraic language and translator for different computing machines in Zürich (ERMETH), München (PERM) and Darmstadt, forming the so called ZMD group. Later, when Bauer and Samelson moved to Mainz (Z22), this group became known as the ZMMD group.(F. L. Bauer, 1990, pp. 46, 47) The first GAMM proposal for the international algebraic language was based on the technique used in the simple calculator described above. At the Zürich meeting, Bottenbruch presented a working compiler for their proposed language. It appeared that the method of translation presented was much more elaborated than the methods known and used by the Americans.(Friedrich L. Bauer, 2002, p. 34) As we have seen earlier, however, Wegstein did know this technique, as did others. The question is: Did he get the idea of the technique on this meeting or was it developed independently by himself? Given the two totally different descriptions of the same technique, it is reasonable that he indeed did develop the same technique independently from Bauer and Samelson.
The origin of the block structure in ALGOL can also be found in the ZMMD effort. It was proposed by Samelson because it was a natural extension of the stack principle of their translation technique.(Friedrich L. Bauer, 2002, p. 35) Unfortunately, the compromise resulting from the Zürich meeting was less focused on the stack principle.(F. L. Bauer, 1990, p. 47) In ALGOL 60, however, the block structure would be one of the basic elements of the language, but now not originating from the stack principle, but from the highly structured definition of the language created by Peter Naur.
After the definition and publication of IAL, the ZMMD group adapted their compilers. Already in 1958, they had working translators for their various machines.(F. L. Bauer, 1990, p. 47) In June 1959, the ICIP conference took place in Paris where Bauer and Samelson presented their translation technique. After this presentation, the ZMMD group expanded into the ALgol COnverteR group (ALCOR). Computer manufactures, research centres and universities from Europe and even one from the USA joined the core group in Germany. All the members got the same information about the ZMMD translators and started working on their own compilers.(Samelson & Bauer, 1960, p. 210)
Meanwhile, Bauer and Samelson published their technique in the Communications of the ACM. The explanation for the influence of this article is twofold. First of all, the translation technique described was the basis of Bauer and Samelson’s proposal for IAL and later ALGOL. As a result, this technique was extremely suitable for translating ALGOL.
The second part of the explanation lies in the moment of publication. It was published some months before the publication of the ALGOL 60 report. This report generated much interest in ALGOL and as a result in the translation of ALGOL. People starting writing their own translators for ALGOL 60 had a suitable basis to start from: the technique described in Bauer and Samelson’s article.
2.2 Sequental formula translation explained
In Sequential Formula Translation, Bauer and Samelson (1960) described the translation technique used by the ALCOR group for their IAL translators. The basis of the technique was still the same as in the design of the simple calculator (see above): incoming symbols are postponed till the first moment they can be evaluated, or in this case, translated. Incoming operators are compared with the topmost operator in the stack using a matrix defining the action to be taken given an incoming symbol and a topmost symbol. The main difference between the design of the calculator and the technique described in this article was that the calculator was to be a device and the translator was a computer program for a general purpose computer.
The technique is explained with an example. In the table
below(Samelson & Bauer,
1962, p. 78)] the algebraic expression \((A \times b + c \times d)/(a -d) + b \times c\) is
translated. The translator uses a symbol stack, initially it is empty.
The program that is generated uses a number stack to calculate (subparts
of) the expression. In this example, the generated program is an ALGOL 60
program, normally it would be an assembly program. array Nis
the number stack. Instead of using a stack pointer, the values of that
stack pointer are used directly for explanatory purposes. Otherwise,
operations on the stack would look like N[n] := b; and the
stack pointer (here n) would be incremented and decremented
when an element is pushed onto the stack or removed from the stack,
respectively.
| symbol stack | next symbol | resulting program |
|---|---|---|
| \([]\) | ( | |
| \([(]\) | a | N[0] := a; |
| \([(]\) | \(\times\) | |
| \([(, \times]\) | b | N[1] := b; |
| \([(, \times]\) | \(+\) | N[0] := N[0] $\times$
N[1]; |
| \([(, +]\) | c | N[1] := c; |
| \([(, +]\) | \(\times\) | |
| \([(, +, \times]\) | d | N[2] := d; |
| \([(, +, \times]\) | ) | N[1] := N[1] $\times$
N[2]; |
| \([(, +]\) | N[0] := N[0] $+$
N[1]; |
|
| \([(]\) | ||
| \([]\) | \(/\) | |
| \([/]\) | ( | |
| \([/, (]\) | a | N[1] := a; |
| \([/, (]\) | \(-\) | |
| \([/, (, -]\) | d | N[2] := d; |
| \([/, (, -]\) | ) | N[1] := N[1] $-$
N[2]; |
| \([/, (]\) | N[0] := N[0] $\div$
N[1]; |
|
| \([/]\) | ||
| \([]\) | \(+\) | |
| \([+]\) | b | N[1] := b; |
| \([+, \times]\) | \(\times\) | |
| \([+, \times]\) | c | N[2] := c; |
| \([+]\) | \(\bot\) | N[1] := N[1] $\times$
N[2]; |
| \([+]\) | N[0] := N[0] $+$
N[1]; |
|
| \([]\) |
For simple arithmetic expressions this method was clear, however, IAL
consisted of more than just simple arithmetic expressions. Other parts of
IAL were translated in a similar way: postponing symbols till they can be
evaluated and translated. For example, the brackets delimiting a compound
statement, begin and end were treated like
arithmetic parenthesis. The end keyword takes care of
evaluating all the remaining symbols on the stack till the
begin symbol is reached.
More problematic were the if and for
statements. Remember, Bauer and Samelson’s article was about translating
IAL: the if statement is like if B; S and the
for statement like for v := L; S. The
; is the syntactical end of the statement, but it is not the
semantical end: effectively, S belongs to the statement.
In the translation of if B;0;S1 the if
symbol is removed from the stack on the encounter of ;0. The
target address for the case B = true is known at this point
in the translation, however, the target address for the case B =
false is still unknown. To solve this problem, an auxiliary
if symbol is introduced during the translation which will be
removed on encounter of ;1 when the target address for the
case is known. In other words, during the translation ;0 is
treated as a kind of then symbol.
for v := L0,L1,...,Ln; sis translated into:
v'[0] := L0; v'[1] := L1; ...; v'[n] := Ln;
for i := 1 (1) k; begin v := v'[i]; S endThe list-of-values variant for statement was translated
into equivalent substatements (see above). The translation of a
start-step-end-variant for statement goes as below. Of
course, if the step is negative, the if statement would test
the opposite. In case the sign of the step is unknown at compile time, it
has to be decided at run time, and the code to decide that, is added
too.
for c := Ei(Es)Ee; Swhere Es is positive, is translated into:
v := Ei; s := Es; e := Ee
L: S; v := c + s; if v ≤ e; goto L; v := v - s;The translation of other elements in the IAL language, like declarations and procedures, were treated as straightforward. For example, procedures were translated as mere subroutines. One element of IAL, however, did get more attention: the . The translation of subscripted variables was not simple. Although Bauer and Samelson treated only static arrays, the computing of the addresses for these subscripted variables needed much explanation. Actually, memory management was one of the hot items in the field of translator writing in these days. The translation of ALGOL 60, especially the implementation of recursion, procedures, and dynamic sized arrays, stimulated the development of dynamic memory management.
3 Implementing procedures and recursion
3.1 “Solving” by ignoring
The publication of the ALGOL 60 report was not the start of implementation of ALGOL languages. For example, in the USA different projects were started to implement algebraic languages, like MAD, NELIAC, and JOVIAL. All these languages were based on IAL, that is, it was not an implementation of IAL itself, but IAL was used as a set of guidelines for their own algebraic languages. In Europe, as said earlier, the ZMMD group was building translators for their proposals for IAL and later for the final draft of IAL too.
Although there was experience with translating IAL-like languages, the
translation of ALGOL 60 was different from the translation of IAL in two
important ways. First of all, there were some elements of ALGOL 60 which
were new and these elements were not seen as useful or understood
completely.@Bauer1962a [215] In particular recursion, the procedure
concept, dynamic sized arrays and own variables were
problematic and led to the development of dynamic storage allocation.
Second, the amount of interest generated by ALGOL 60 was much bigger than generated by IAL. Many more implementations were started after the publication of the ALGOL 60 report than were started after the publication of the report on IAL.
The ALCOR group started an implementation of ALGOL 60 based on their
translator for IAL. Instead of implementing the new programming language
concepts, however, they decided to ignore these difficult features.
Conditional boolean expressions, conditional designational expressions,
the while part in the for statement,
own declarations and recursive procedures were not part of
the early ALGOL 60 translators of the ALCOR group.
Instead of focussing on implementing the whole language the ALCOR group tried to maximise intercompatibility between the computers of the members of the ALCOR group. All members used the same hardware representation and most of them also used the same translation technique as described above. The translation matrix controlling the method was given to all the members to assure that the same semantics were implemented at all the different installations. As a result, programs written for one member’s computer could run on all member’s computers.(Bumgarner & Feliciano, 1963, p. 597) Later, their translators became more feature complete, but the pioneers of implementing these features were working outside the ALCOR group.
Ignoring difficult or useless features was not uncommon. According to
a questionaire in the ALGOL Bulletin no. 9, the
own declaration was almost always omitted.(Naur, 1960) Outside the ALCOR
group, more than half of the compilers did not include variable size
arrays.(Naur, 1960)
Interestingly, all the non-ALCOR compilers in this questionaire did
include procedures.(Naur,
1960) Either they did not mention recursion or it was fully
implemented.
Although recursion was not implemented by the ALCOR group, it was one of the new interesting and controversial concepts in ALGOL 60. As said before, many people did not see why it would be useful at all. Others, however, did see the theoretical importance of the concept.(E. T. Irons & Feurzeig, 1960, p. 1) In 1960, two articles on the implementation of recursive procedures were published.
3.2 Dijkstra’s Recursive Programming
The first and most influential article of the two was Recursive Programming Dijkstra (1960) by E.W. Dijkstra. It was published in the second issue of Numerische Mathematik in 1960. As said before, his implementation of recursive procedures was developed during the development and implementation of the ALGOL 60 compiler for the Electrologica X1 at the Mathematical Centre in Amsterdam.
Dijkstra based his method of implementing recursion on the translation technique of Bauer and Samelson because it was ‘well known (…) and so elegant that we could not refrain from trying to extend this technique by consistent application of its principles.’(Dijkstra, 1960, p. 313) Actually, he made the observation that it does not matter if an simple expression is evaluated or that an expression containing a procedure call is evaluated. Both evaluations will use the next free places on the stack to compute the resulting value. Hence, procedures can be treated like expressions with keeping some extra administration.
The translator uses the stack for computing intermediate results only. Values needed are pushed onto the stack and are used when a subexpression can be computed. Then, the values used are removed and replaced by the value of the expression. However, when a procedure is called the parameters and local variables of the procedure are pushed onto the stack. Because these elements must be accessible later, access to elements deeper down in the stack is needed. For this reason a more elaborated stack was needed instead of the simple stack used for calculating simple expressions.
The program text is stored in memory, instruction after instruction this program is executed, using the stack to compute intermediate results. When a procedure is called, the normal flow of instructions changes because the static program text of the procedure is located somewhere else in memory. Furthermore, the dynamic part of the procedure is pushed onto the stack. This dynamic part consists of the parameters, the local variables and the link data. This link data defines the state of the execution of the program in which the procedure is called, and is used to return back to the normal flow of the program where it was when the procedure was called.
The execution of the procedure program text also uses the stack in the same way the main program did: for computing intermediate results and for calling procedures. This execution starts on the first free place on the stack, directly after the places where the parameters and local variables of the procedure are stored. If another procedure is called, the same thing happens, the current situation is stored as part of the call and is pushed onto the stack with the dynamic data of the new procedure. This procedure is then executed. When the execution ends, the old situation of the previous procedure is restored, and execution of that older procedure goes on. Eventually, this procedure is also finished, the state of the main program is restored and execution of the program goes on. Of course, more than two procedures can be called, even recursively.
As part of the link data, a block number is stored to be able to access global variables with respect to this block. Initially, the block number is zero. In addition, two parameter pointers, a return address and the stack pointer are stored as part of the link as well. This approach was also used to execute blocks. These were treated as procedures without any parameters or return value.
3.3 The solution of Irons and Feurzeig
Another way of implementing procedures was published in 1960 by
E.T. Irons and W. Feurzeig in Comments on the
Implementation of Recursive Procedures and Blocks in
Algol-60@Feurzeig1960a. Where Dijkstra only used text to describe
his method of implementing recursive procedures, Irons and Feurzeig were
also using flow diagrams to exemplify things. They treated blocks,
procedures, and the goto statement together because these
concepts change the normal flow of execution of a program. Again, the
translation of both procedures and blocks are more or less similar. The
way of handling blocks is just somewhat simpler because less information
has to be checked and stored.
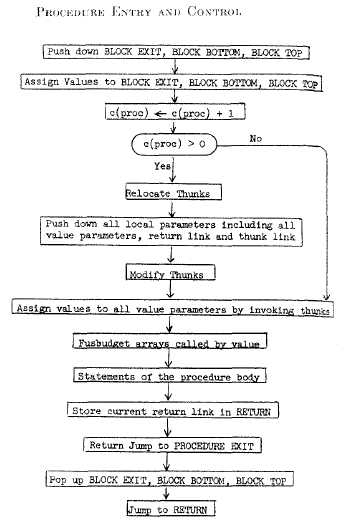
The procedures and blocks are handled by special entrance (see Figure [procedureentryandcontrol]) and exit (see above Figure) routines which are executed by entering a block (or procedure) and by exiting them. Procedures are treated as blocks where the return link and thunk link are stored as local variables. Thunks are a way to get the address of a parameter into a standard location, regardless the parameter type.(Ingerman, 1961) Interestingly, J. Jensen and Peter Naur (1961) give in An implementation of ALGOL 60 procedures(Jensen & Naur, 1961) a more or less similar implementation of handling different parameters in procedures.
Furthermore, three pointers are used to point to the current active
block: block exit points to the exit routine, block
bottom points to the lowest memory address of the active block and
block top points to the highest memory address of the active
block. These pointers are comparable to the procedure pointers in the
link data used by Dijkstra.
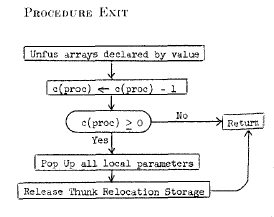
Instead of a block number, however, there is a recursion counter. For
every procedure c( proc ) denotes the recursion depth.
Initially, the recursion counter is -1. Because procedures
can be recursive and blocks can not, this counter is used for procedures
only.
Both methods of implementing recursion were very similar. When a block is executed, the current situation is stored, local variables, including parameters, are pushed onto the stack and the exectution of the block starts. By the end of the execution, the old situation is restored. As for the handling of procedure parameters, here too, both Jensen and Naur’s, and Ingerman’s method are very similar. The extensions to the technique to implement the more difficult concepts in ALGOL 60 were more or less straightforward and fitted easily into the technique of sequential formula translation.
4 The influence of ALGOL’s structure
Besides extending the common translation technique, two other approaches to the translation of ALGOL were undertaken. These approaches, improving the existing translation techniques and inventing new translation techniques, are now discussed.
Although most of the efforts in these approaches started differently the focus was the same: on the structure of the language or the structure of the notation used to describe the language. The highly structured definition of ALGOL 60 in the ALGOL 60 report combined with the use of the BNF caused a growth in interest in syntax of programming languages and the structure of translators. As a result, several syntax directed translators and translation techniques were developed.
The ideal was a program that, given a definition of a language in a metalanguage like BNF extended with some semantical information, could generate a translator. One such a translator was developed by Brooker and Morris for the ATLAS computer. This ‘Assembly Program for a Phrase Structure Language’(Brooker & Morris, 1960, 1961), however, was developed outside of the ALGOL effort. Nonetheless, Brooker and Morris may have influenced some of the scientists discussed below because of the many publications on their translation program.
In January 1961, the issue of the Communications of the ACM was dedicated to the translation of algorithmic languages. From the seven articles on the translation of ALGOL, two were on the translation of ALGOL in relation to the structure of ALGOL 60 itself: Recursive Processes and ALGOL Translation(Grau, 1961) by A.A. Grau and A Syntax DIrected Compiler for ALGOL 60 by E.T. Irons.
4.1 Grau’s recursive translation technique
In his article, A.A. Grau improved the translation technique described by Bauer and Samelson by reducing the size of the translation matrix. This matrix, as said earlier, defined the action to be taken given an incoming symbol and the topmost symbol on the stack. Because ALGOL 60 consisted of many symbols this matrix was large. Given the small amount of memory computing machines were equipped with in those days, this was problematic, especially for the many small scale computers in use in Europe.
An important aspect of ALGOL’s description was its recursive definition. Grau tried to reflect this recursive structure on the translator: if there is a statement, it should be translated by a statement procedure, a expression by an expression procedure, etc. However, because statements can be recursive, a procedure must be able to call itself. So the translator itself should be recursive. In fact, the translator only translates blocks because blocks are the basic elements of an ALGOL 60 program. All other elements are translated by dedicated procedures called by this block procedure.
These recursive procedures are called when the translator reaches a
state when the with the procedure corresponding elements are expected.
For example, if the translator is in a state where an arithmetic
expression is expected, and the next input symbol is an if
symbol, then the translator pushes, according to the definition of the
ALGOL 60 arithmetic conditional expression:
<arithmetic expression> ::= if <boolean expression> then <simple ae>
else <arithmetic expression>the next state onto the stack, that is the state and calls the boolean
expression procedure. After translating the boolean expression, the top
most element of the stack will be this then-part state.
The description of Grau’s technique is difficult to understand because Grau (1961) used recursive procedures which were to be implemented using a stack. In his technique the recursive descent parsing technique can, however, already be recognised.
4.2 Irons’s syntax directed compiler
Another approach to the problem of translating ALGOL, independent of the techniques used in the ALCOR group, was one developed by E.T. Irons and published as A Syntax Directed Compiler for ALGOL 60(Edgar T. Irons, 1961) in 1961. Later, in 1963, an extended version of the article was published as The Structure and Use of the Syntax Directed Compiler(Edgar T. Irons, 1963). According to Irons, the problem of early compilers was that the function of translation of the language and the function of definition of the language were mixed into one program. He wanted to separate the two functions by using an extended metalanguage to define a programming language and a general translator program to translate programs written in that newly defined programming language using the definition of that language.
This metalanguage consists of a set of rules defining both syntax and
semantics. These rules have the form syntax =:: S → {semantics} .
S, a syntactic unit, is the subject of the rule. The syntactical
part of the rule consists of syntactical units, similar to the BNF. The
semantical part is a list of semantical definitions which can have three
different forms: symbols in the output language, substitution of output
symbols for other output symbols, and functions on output symbols.
The translator works by using definitions, as described above, to translate a program text into the target language. Starting at the bottom, from left to right, syntactic units are recognised and the semantic rules are applied till an topmost element is recognised and no further steps can be taken.
In March 1962, Robert S. Ledley and James B. Wilson published Automatic-Programming Language Translation Through Syntactical Analysis(Ledley & Wilson, 1962), describing an approach to the general problem of translation based on the work of Irons (1961). The metalanguage used by Irons was changed a bit: the syntactical element of the rule is put in front, followed by the syntactical part and then the semantical part. In addition, the semantical part was made more understandable. The underlying technique, however, was the same.
4.3 Lucas’s structure of formula translators
In September 1961, P. Lucas published The Structure of Formula-Translators(Lucas, 1961) in the supplement number 16. He, as did Grau (1961), based his work on Bauer and Samelson and tried also to improve the technique by reducing the translation matrix. Although the technique was developed while implementing an ALGOL 60 translator(Lucas, 1961, p. 1), the article had a more general claim: it presented a technique for algebraic translators in general.
Using three levels of meta language: the object language, the language
used in the ALGOL 60 report, and a generalised version of the same
language using Greek letters between double angular brackets, a new
language was defined. This third level metalanguage is used to describe
patterns of elements in the second level metalanguage. For example, the
pattern underlying <integer> ::= <digit> |
<digit> <integer> is <<β>> ::=
<<α>> | <<α>><<β>>.
Lucas now distinguished three types of syntactical definitions:
enumerations, juxtapositions and combined definitions. In all three
groups there are two variations: explicit and recursive definitions.
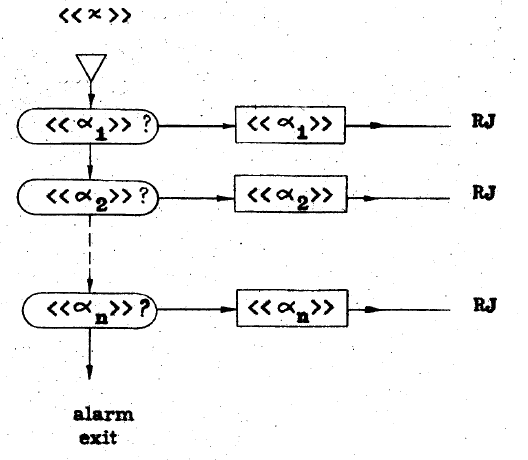
Enumerations have the form <<χ>> ::= <<α0>>
| <<α1>> | <<α2>> | ... |
<<αn>> and form a so called syntactic category. The
lefthand side variable can be replaced by one of the variables on the
right hand side.
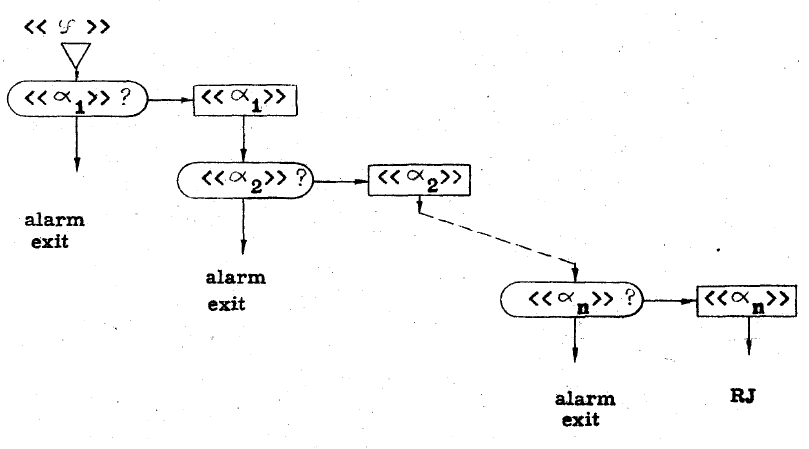
The juxtaposing definition looks like <<χ>> ::=
<<α0>><<α1>><<α2>>...<<αn>>.
The left hand side variable may be replaced by the whole right hand side.
The combination group is, of course, a combination of the other two
groups.
A definition is explicit if a left hand side variable does not occur
in any (sub)part of a right hand side variable. In recursive definitions,
however, left hand side variables does occur in the right hand side
variables or subparts of it. Lucas does denote this with
cont(<<χ>>, <,β>>), that is,
<<α>> does occur in
<<χ>>.
Lucas presented for every group of definitions the structure of the translation procedure. In Figures above the program structure of respectively enumerating and juxtaposing definitions are presented. A rounded box denotes the question: Is the incoming symbol the element inside the box? If so, that element is translated, indicated by a box with the name of the element in it.
In fact, first is tested if the expected element is indeed found. If so, the translation procedure of that element is called. These two Figures give the explicit structure. If a definition is recursive, the structure changes as expected: a loop is introduced. The whole translator consists of recursive procedures calling each other according to the structure of their definitions. Of course, some extra administration is added to the structure of the procedures. In essence, however, this is the whole technique. Here too, as in the case of Grau (1961), the later recursive descent parsers can already be recognised.
4.4 Connecting ALGOL-like languages with context-free language theory
Interestingly, both Grau (1961) and Lucas (1961) arrived at similar ideas when they both try to improve the translation technique of Bauer and Samelson. The same happened in the case of Dijkstra (1960), and Feurzeig and Irons (1960) with implementing procedures and also with Jensen and Naur (1961) and Ingerman (1961) with their implementation of the different types of parameters in procedures. Somehow, independent from each other, the same developments were made. This can be a sign of an immature scientific infrastructure. On the other hand, it can also be a sign of how well the translation technique, theory and language fitted together.
In addition, the terminology and notation used was not consistent throughout the different articles. That is another sign of the evolving field of translator writing: a common basis had to be found. One big step towards a common base was made by Ginsburg and Rice (1962). They wanted to get more knowledge about programming languages because these languages were becoming more and more important for instructing computers. To that end, they abstracted from ALGOL and developed two models of similar programming languages: definable languages and sequentially definably languages.(Ginsburg & Rice, 1962, p. 350) The former are languages defined by the BNF where all left-hand side elements are metalinguistic variables. This set of languages are equal to the type 2 languages defined by Noam Chomsky in 1956: the context-free languages.
As a result, Ginsburg and Rise (1962) not only tried to formalise ALGOL-like languages, they also made the connection between programming languages and theoretical linguistics. This connection turned out to be a fruitful one. The field of formal languages, the definition of programming languages, and translation became a very popular one. Soon after the publication of Two Families of Languages Related to ALGOL in 1962, publications in the field of translator writing became more and more theoretical.
With this formalisation the field of programming languages could be fit into the theory of computing and automata theory, developed in the 1940s and 1950s.(Mahoney, 1997) In other words, the practice gained with programming computers and with programming languages could be based on a theoretical foundation. The field of computing became a real science in the sense that it got its own theoretical component connecting practice and theory: theoretical computer science.
5 Conclusion
This chapter started with the question what part of the ALGOL effort was the most influential. The answer lies in the fact that the ALGOL effort was a catalyst for the field of translator writing: it transformed this field from a craftsmanship to a science. This transformation started with the development and publication of a translation technique for IAL by Bauer and Samelson, who initiated the ALGOL effort to construct a translation technique and matching language simultaneously.
The language was made to fit the technique, and vice versa. When Bauer and Samelson, some months before the publication of the ALGOL 60 report, published their technique, it was widely read. Because of the popularity of ALGOL 60 many implementations of ALGOL 60 translators were started, often based upon the technique described by Bauer and Samelson. During this process, the isolated efforts to create an algebraic language became part of a larger effort: the ALGOL effort.
Although there was a translation technique for IAL, some elements of ALGOL 60 requested the extension of the technique (notably the implementation of recursion and procedures by Dijkstra (1960), and by Feurzeig and Irons (1960)). Both groups came to similar solutions, fitting into the well-known translation technique.
Other approaches to the translation of ALGOL were improving the technique and inventing new techniques. Both Grau (1961) and Lucas (1961) improved the technique by tackling the size of the translation matrix. Both arrived to a solution with recursive procedures in which the later recursive descent parsing technique can be recognised.
Irons (1961) invented a new technique of translation based on the structure of ALGOL. From left to right, from bottom to top, his technique was based on a metalanguage in which both syntax and semantics were to be specified. A general translator was then able, with these specifications and a program text, to translate the program into a executable version.
Although these approaches to develop syntax directed translators were different, the lack of a common notation, terminology, or theory was striking. Clearly, the field missed a sound theory to be able to evolve from a craft into a science. Ginsburg and Rice (1962) supplied the field with this theory: they created the connection between Chomsky’s (1956) context-free languages and ALGOL-like languages and hence connected the field of programming languages with other theories of computing and automata theory.
The further development of the field of translator writing, although related to ALGOL at first, was no longer ALGOL centred. It became an independent field of research, with an own vitality, evolving freely from the ALGOL effort. But what was the most influential part of the ALGOL effort for the transformation of the field of translator writing? Bauer and Samelson’s translation technique or the structured definition of ALGOL 60? Or the whole ALGOL effort as it created a common notation, theory and technique?
