Het gebruik van computers op het Mathematisch Centrum
Huub de Beer
Amsterdam, 26 februari 2008
De ontwikkeling van het computergebruik op Rekenafdeling
De Rekenafdeling was al vanaf het begin bezig met de constructie van automatische rekenmachines. Het zou toch nog tot 1954 duren voordat zo’n automatische rekenmachine werd ingezet voor praktisch rekenwerk bij rekenopdrachten. Tot die tijd werden de rekenopdrachten uitgevoerd door de wiskundigen en rekenmeisjes van Van Wijngaarden. Zij waren de rekencapaciteit die de Rekenafdeling ter beschikking had, ondersteund door elektronische tafelrekenmachines, telmachines, een aangepaste boekhoudmachine en vanaf halverwege 1953 ook ondersteund door een ponskaarteninstallatie.
Tussen 1950 en 1952 werd de automatische rekenmachine ARRA getest en voerde daartoe een viertal rekenopdrachten uit: het berekenen van tabellen van een aantal functies zoals \(x^{-2}\). Voor veel praktisch rekenwerk werd deze machine nooit ingezet. Pas bij het in gebruik nemen van de herziene versie van de ARRA in 1954 deed de computer zijn intrede bij het uitvoeren van rekenopdrachten. Langzaamaan nam de computer een steeds prominentere plek in bij de uitvoering van rekenopdrachten. Deze ontwikkeling van het computergebruik door de Rekenafdeling wordt weergegeven in de tabel hierboven. De tabel is gebaseerd op de jaarverslagen van het Mathematisch Centrum waarin tot 1961 alle uitgevoerde opdrachten kort beschreven werden, daarbij werd meestal ook vermeld of een computer was ingezet bij de uitvoering van die rekenopdracht. Vanaf 1961 werd deze beschrijving weggelaten, maar werd wel vermeld dat bijna alle opdrachten met behulp van de Electrologica X1 computer werden uitgevoerd. De Rekenafdeling was fundamenteel van karakter veranderd, het was een open-shop computer service centrum geworden, gespecialiseerd in geavanceerd technisch-wetenschappelijk rekenwerk.
| jaar | R | \(\Delta\)R | O | MC | +MC | eigen | ARRA I | ARRA II | ARMAC | X1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1946 | ||||||||||
| 1947 | ||||||||||
| 1948 | ||||||||||
| 1949 | 64 | 64 | 39 | |||||||
| 1950 | 114 | 50 | 52 | 27 | 6 | 2 | ||||
| 1951 | 166 | 52 | 59 | 21 | 8 | 1 | ||||
| 1952 | 206 | 40 | 48 | 17 | 13 | 1 | ||||
| 1953 | 249 | 43 | 52 | 13 | 9 | |||||
| 1954 | 297 | 48 | 59 | 8 | 7 | 8 | ||||
| 1955 | 340 | 43 | 53 | 13 | 13 | 20 | ||||
| 1956 | 394 | 54 | 60 | 9 | 3 | 7 | 5 | 13 | ||
| 1957 | 467 | 73 | 73 | 9 | 3 | 5 | 38 | |||
| 1958 | 514 | 47 | 57 | 5 | 3 | 5 | 28 | |||
| 1959 | 557 | 43 | 55 | 6 | 2 | 4 | 17 | 2 | ||
| 1960 | 605 | 48 | 69 | 7 | 5 | 1 | 42 | |||
| 1961 | 725 | 120 | 122 | 11 | 32 | 1 | 122 | |||
| 1962 | 852 | 127 | 179 | 179 |
In verhouding tot het aantal opdrachten dat de Rekenafdeling uitvoerde, was tot 1960 het aantal opdrachten dat met behulp van een computer werden opgelost nooit groter dan de helft. Met andere woorden, de wiskundigen en rekenaarsters bleven tot eind jaren ’50 een belangrijke rol spelen op de Rekenafdeling. Toch kan hieruit niet geconcludeerd worden dat de Rekenafdeling weinig van computers gebruik maakte.
De computers werden niet gebouwd om de rekenmeisjes met tafelrekenmachines te vervangen, die voldeden namelijk uitstekend. Nee,
de problemen, waarbij de machtigste der moderne machines pas goed tot hun recht komen, zijn dusdanig omvangrijk, dat men er zonder deze rekenapparatuur nooit aan zou zijn begonnen! Er worden problemen mee aangepakt, die vroeger de meest drieste niet eens als “numeriek probleem” zou durven te beschouwen; en inderdaad, naarmate de methoden, waarop de machines hun resultaten afleveren, geraffineerder worden, raakt het numeriek karakter althans voor de naïeve bezoeker, ernstig op de achtergrond.1
Een van de eerste opdrachten die met de herziene ARRA werden uitgevoerd was het berekenen van moleculaire golffuncties van waterstof, deuterium en tritium voor het Instituut voor Theoretische Natuurkunde van de Universiteit van Amsterdam. Daarnaast werden matrixberekeningen van matrices met 23 rijen en kolommen voor Fokker uitgevoerd en voor een scheepsbouwer enige berekeningen aan scheepsschroeven.2 In de volgende jaren werd de ARRA onder andere ingezet voor flutterberekeningen voor Fokker, uitrekenen van grote tabellen, meerdere matrixberekeningen, getijdeberekeningen voor de Delta-commissie, het rekenen aan kernreactoren en de berekening van frequenties voor onderzeese telefoonkabels.3
De reden dat besloten werd om snel de ARMAC te gaan bouwen, was het gebrek aan rekencapaciteit van de ARRA. Wederom werden de grenzen van wat de Rekenafdeling praktisch kon berekenen opgeschoven met een nieuwe machine. De ARMAC werd ingezet voor getijdeberekeningen voor de Delta-commissie en voor het berekenen van het dynamische gedrag van de Haringvlietsluizen4; het Mathematisch Centrum verrichte veel rekenwerk werk in het kader van de Delta-werken.
Vanaf de oprichting van de Rekenafdeling op 1 december 1947 en de eerste rekenopdrachten werden uitgevoerd, was deze serviceverlening een succes. De verwachte inkomsten uit deze rekenopdrachten zouden zeker gehaald worden.5 De Rekenafdeling had ten doel rekenwerk te verrichten ten dienste van wetenschap, overheid en industrie. Een deel van de opdrachtgevers, voornamelijk uit wetenschappelijk hoek, hoefde voor het verleende rekenwerk niet te betalen.
Zelfs met veel niet betalende opdrachtgevers was het Mathematisch Centrum in staat om met behulp van hun computers veel inkomsten te genereren. Deze inkomsten bestonden voor een deel uit het verkopen van know-how over de constructie van computers aan Fokker en Electrologica. Daarnaast bracht het verhuren van computertijd op de ARMAC en X1 veel geld op. De ARMAC, met een prijs van 100 gulden per uur, bracht in de vier jaar dat de machine in gebruik was, ongeveer 190.000 gulden op.6 De X1 bracht nog veel meer op; alleen al in het eerste jaar dat deze computer in gebruik was genereerde de machine 143.845,50 gulden à 300 gulden per uur.7 Door deze inkomsten was het Mathematisch Centrum in de jaren ’50 en ’60 in staat om zich steeds grotere en sneller computers te verwerven en zo haar leidende positie in Nederland op dit gebied vast te houden.
Groei van het computergebruik
Het computergebruik op de Rekenafdeling groeide bij elke nieuwe computer die in gebruik werd genomen. Niet alleen in het aantal opdrachten dat ermee werd uitgevoerd, of wat betreft de hoeveelheid rekenwerk, maar ook wat betreft het aantal gebruikers en de bruikbaarheid van de computer. De ARRA vergde relatief veel onderhoud en was langzaam. Om de machine ten volle te benutten, werd de computer dag en nacht gebruikt. Bij de ARMAC veranderde dat allemaal. Deze machine was zoveel betrouwbaarder en sneller, dat er geen nachtdiensten meer nodig waren. Ook het aantal gebruikers groeide, veel opdrachtgevers gingen nu zelf hun programma’s schrijven en lieten ze uitvoeren op de ARMAC.8 Bij het in gebruik nemen van de X1 zette deze trend zich nog verder door.
De bruikbaarheid van de computers, de toename van het gebruik en het aantal gebruikers werd ook gereflecteerd door de software die beschikbaar was voor de opeenvolgende machines. De machineprogrammering veranderde niet fundamenteel. Natuurlijk, elke computer was complexer dan de vorige, had nieuwe functionaliteit en dat was ook zichtbaar in het aantal machineopdrachten. Een voorbeeld daarvan zijn de machineinstructies van de ARMAC om blokken geheugen van het ene geheugen naar het andere te transporteren. Deze instructies waren nodig omdat de ARMAC over een klein snel buffergeheugen beschikte naast een groot langzaam geheugen.
Machineprogrammering was lastig en het invoerprogramma ondersteunde de programmeur bij het programmeren. Het bood allerlei faciliteiten, zoals het invoeren van decimale getallen en een vorm van relatieve adressering. Daarnaast werd tijdens het gebruik van de machine een bibliotheek van bruikbare subroutines opgebouwd waarmee de programmeur eenvoudig en snel allerlei functionaliteit in zijn programma kon opnemen, bijvoorbeeld bepaalde wiskundige functies zoals de sinus of worteltrekken.
Daarnaast waren er ook standaard subroutines. De meest belangrijke subroutines waren wel de in- en uitvoerroutines. Met behulp van de uitvoerroutine kon de programmeur getallen netjes uittypen op de aan de computer aangesloten typemachine. Deze in- en uitvoerroutines werden in de loop van de tijd steeds betrouwbaarder en kregen meer functionaliteit. Voor een deel doordat ook andere uitvoerapparaten werden aangesloten, zoals een bandponser, waarna deze uitvoerroutines ook een band konden ponsen. Deze uitvoerroutines of typeroutines voor de ARMAC maakten het zelfs mogelijk om de layout van de pagina te controleren bij het uittypen van getallen.
Andere standaard subroutines voor de ARRA waren Rd1 en Rd2 waarmee berekeningen met getallen met een drijvende komma eenvoudiger werd gemaakt. In de ARRA werden breuken voorgesteld door de komma gevolgd door een vast aantal cijfers achter de komma. Voor veel toepassingen voldeed dit, al dan niet na schalen, prima. Voor een aantal toepassingen waren vaste komma breuken echter vreselijk onhandig. De oplossing: drijvende komma getallen. Maar de ARRA, net als de ARMAC en de X1 overigens, kende geen drijvende komma getallen. Nu was het mogelijk om met behulp van deze twee subroutines, Rd1 en Rd2, toch met drijvende komma getallen te rekenen op de ARRA.
Bij elke operatie op een drijvende komma getal moest de programmeur wel de subroutines aanroepen, een lastig karwei. Voor de ARMAC schreef Dijkstra daarom het interpretatief programma Rd1 waarmee een nieuwe machine werd gesimuleerd die wel met drijvende getallen kon rekenen en daarvoor gewoon machineopdrachten had. Deze nieuwe pseudomachine kon als het ware aangezet worden door een bepaalde subroutinesprong waarna alle volgende instructies werden geïnterpreteerd als machineinstructies van die pseudomachine. Op eenzelfde wijze kon de pseudomachine weer verlaten worden.
Naast een interpretatief programma voor het rekenen met drijvende komma was er voor de ARMAC ook een interpretatief programma voor het rekenen met complexe getallen met drijvende komma’s, een interpretatief programma voor het rekenen met zesvoudige lengte getallen en een interpretatief programma voor het rekenen met breuken van dubbele lengte. Daarnaast waren er meer standaard subroutines, bijvoorbeeld ook voor een aantal veelgebruikte wiskundige functies. Tenslotte was er het matrix-complex RAM, een verzameling subroutines om met matrices te rekenen.
Deze ontwikkeling van een groei in bruikbaarheid, een groei in de hoeveelheid software en het aantal gebruikers was er een die zich zelf versterkte. Doordat de machine bruikbaarder werd, was het mogelijk om meer en betere software te leveren waardoor de machine weer meer bruikbaarder werd. Doordat de machines bruikbaarder werden, kwamen er meer gebruikers, waardoor het verantwoord was meer software te schrijven. Ook bij het in gebruik nemen van de X1, zette deze trend zich door, onder andere met een ALGOL 60 compiler.
Van wiskundig probleem tot programma
Naast een ontwikkeling in computerbouw, computergebruik en software vond er op de Rekenafdeling ook een ontwikkeling in het programmeren plaats. In de rapporten over de verschillende machines werden aanwijzingen gegeven hoe er werd geprogrammeerd. Daarnaast werd in 1955 voor het eerst de cursus Programmeren voor automatische rekenmachines9 gegeven voor een breder publiek. Deze cursus ging in op het programmeren in het algemeen, maar behandelde wel een aantal aspecten van de ARRA. Deze cursus werd twee jaar later herhaald, waarbij de ARMAC de plaats van de ARRA innam.
De Rekenafdeling stond in het teken van het rekenen, van het uitvoeren van geavanceerd technisch-wetenschappelijk rekenwerk voor de andere afdelingen van het Mathematisch Centrum en voor derden uit industrie, wetenschap en overheid. De bouw van automatische rekenapparaten, maar bovenal het gebruik ervan stond dan ook in het teken van geavanceerd wetenschappelijk rekenwerk en bouwde voort op de al bestaande traditie van handmatig rekenwerk. De computer en het programmeren werden dan ook vanuit het perspectief van de rekenaar met een handrekenmachine geïntroduceerd.
In het allereerste rapport, Programmeren voor de A.R.R.A. uit 1951 werd uitgelegd wat een woord was, dat het op verschillende manieren geïnterpreteerd kon worden: als een geheel getal, als een breuk, als een opdracht en als een code. De notatie waarin programma’s in machinecode werden opgeschreven is eenvoudig: een adres gevolgd door de combinatie opdracht/numeriek gedeelte of een getal. In de rechter kantlijn was plaats voor uitleg.
Een sprong in het programma verduidelijkte je als programmeur met pijltjes, in de linker kantlijn schreef je naast de inkomende pijlen het adres vanwaar gesprongen werd, in de rechter kantlijn schreef je enkel een pijl waarmee je aangaf dat het een sprongopdracht betrof. Schreef je een dubbele pijl in de rechter kantlijn dan betekende dat het een niet-conditionele sprong betrof. Om de inhoud van een adres aan te geven, schreef je dat adres tussen haakjes.
In de computer waren alle gegevens natuurlijk binair, ook instructies. Gelukkig ponste je als programmeur in de zogenaamde programmeurscode waar je gewoon met decimale getallen kon werken. Elke regel die je ponste had dezelfde vorm: beginletter, getal en eindletter. Het was gebruikelijk om het programma tussen twee twee verticale lijnen te typen waar dan aan beide kanten het programma geannoteerd kon worden met regelnummers, sprongpijlen en uitleg.
Ponste je een opdracht dan was de beginletter eenvoudigweg het opdrachtnummer. Als je echter een getal ponste dan begon je met het teken van dat getal. Voor breuken en gehele getallen waren verschillende tekentoetsen. Tenslotte kon je het invoerprogramma speciale instructies geven, bijvoorbeeld waar de volgende regels te bewaren en dan begon jet met de beginletter “A”. Het getal was het numerieke gedeelte van een opdracht, de absolute waarde van een getal of een adres. De eindletter was bedoeld voor relatieve adressering, de verschillende eindletters kregen voor gebruik een waarde toegewezen en die waarde werd als het beginadres gebruikt voor de reeks opdrachten die werden afgesloten met die eindletter.
Een belangrijk onderdeel van het programmeren was het gebruiken en het maken van subroutines. Standaard subroutines waren van hoge kwaliteit en je kon ze keer op keer hergebruiken. Een subroutine kon je gewoonweg overnemen in je programma wanneer je de subroutine uit wou voeren. Dergelijke subroutines werden “open subroutines” genoemd. “Gesloten subroutines” daarentegen stonden op zichzelf en maakten geen deel uit van het programma, ze werden enkel aangeroepen door het programma. Bij het gebruik van dergelijke subroutines was het gebruik van sluitletters onontbeerlijk.
Bij gebruik van een subroutine diende je als programmeur namelijk een voorponsing te doen waarin je aangaf waar de subroutine in het geheugen kwam te staan en wat de parameters waren. Hierna kopieerde je de subroutine automatisch met behulp van de reproduceerpons. Een subroutine werd aangeroepen met een speciale combinatie van opdrachten waarmee het terugkeeradres in het register A werd geplaatst dat dan door de subroutine zelf achteraan als laatste opdracht van de subroutine werd geplaatst. Dit was de zogenaamde koppelopdracht.
In dit rapport uit 1951 werd dus wel uitgelegd hoe een programma er uit zag en hoe subroutines gebruikt konden worden. Over het programmeren, het omzetten van een wiskundig probleem in een programma dat dat probleem oploste, werd echter niets gezegd. Bij de rapporten over de herziene ARRA werd daar wel iets over gezegd: in Functionele beschrijving van de ARRA was het hoofdstuk ‘De taak van de programmeur’ toegevoegd. Het programmeren bestond uit vijf stappen opgedeeld:
\(1^e\). mathematische formulering van het probleem,
\(2^e\). mathematische oplossing van het probleem,
\(3^e\). keuze of constructie van numerieke processen, die (in het licht van \(2^e\)) tot het gewenste antwoord leiden,
\(4^e\). programmering: gedetailleerde opbouw van de onder \(3^e\) genoemde processen uit de elementaire bewerkingen, waartoe de machine in staat is,
\(5^e\). codering: uitschrijven van het programma in de code der machine, zodat hierna de band onmiddellijk geponst kan worden.10
Verder noemde Dijkstra een zestal idealen die nagestreefd werden bij het programmeren: maximale snelheid, minimale geheugenruimte, maximale veiligheid, maximale accuratesse, maximale souplesse en maximale overzichtelijkheid.11 De kwaliteit van het programma, zowel voor de machine als voor de programmeur, was dus een belangrijk aspect van het programmeren. Daarna werd een typisch programma gekarakteriseerd: het bestaat uit een aantal opdrachten die herhaaldelijk uitgevoerd worden. Eigenlijk was dit ook een karakterisatie van een automatische rekenmachine: het automatisch uitvoeren van veel berekeningen.
Naast algemene opmerkingen over het programmeren werd ook de notatie van programma’s in dit rapport uitgebreid. De verschillende interpretaties van een woord kon je met verschillende haakjes aangegeven. De inhoud van het adres \(x\) schreef je als (\(x\)); (\(x\)) geïnterpreteerd als een geheel getal schreef je met vierkante haken en een breuk met accolades. In een woord van de herziene ARRA pasten twee opdrachten. Wilde je aangeven dat een adres als die twee opdrachten moest worden geïnterpreteerd, dan schreef je dat met \({<}x{>}\). Met behulp van deze notatie kon je je programma’s korter en overzichtelijker uitleggen. Een andere manier om je programma’s overzichtelijk weer te geven was een blokschema.
De notatie van programmeurscode veranderde ook iets bij deze nieuwe machine. De sluitletters waren nu geen getallen meer maar de letters X en A tot en met F. Daarnaast was er een vierde element op een regel bijgekomen: de kanaalcorrectie, die je alleen bij het invoeren van een adres kon gebruiken. Met de kanaalcorrectie selecteerde je het kanaal op het trommelgeheugen waar de je de geponste regel wilde wilde opbergen.
Het denken over programmeren
In de twee handboeken voor de FERTA werd niets gezegd werd over het programmeren in het algemeen, enkel de machine zelf werd beschreven. Hetzelfde gebeurde bij de beschrijving van de ARMAC. Dit betekende overigens niet dat het programmeren geen belangrijk onderwerp meer was, integendeel. In 1955 werd de eerste cursus programmeren voor automatische rekenmachines gehouden en eind 1957 de tweede. De cursussen behandelden het hoe en wat van het programmeren zeer uitgebreid. Het programmeren werd hiermee losgemaakt van het bedienen van een speciale machine. De cursussen dienden niet om specifiek te leren werken met de machine van de Rekenafdeling, alhoewel die machines wel gebruikt worden als de voorbeeldmachine tijdens de cursus: programmeren zat immers nog dicht bij de machine.
Na een viertal algemene introducerende hoofdstukken waarin achtereenvolgens automatische rekenmachines, woorden, getallen en opdrachten besproken werden, ging de cursus verder met blokschema’s (flow diagrammen). Blokschema’s waren belangrijk om de leesbaarheid en begrijpelijkheid van je programma’s te verbeteren: ‘Voor de geïnteresseerde, die het programma inkijkt, zelfs voor de programmeur, die het programma opgesteld heeft, houdt deze “verstaanbaarheid” echter niet over: het lezen van een programma van de opdrachten alleen, zonder een blik te slaan in de explicatie, die er gelukkig doorgaans wel naast staat, vergt erkend veel geduld en doorzettingsvermogen.’12
De leesbaarheidsproblemen werden vooral veroorzaakt doordat er veel opdrachten nodig waren om duidelijk afgebakende eenheden van functionaliteit te beschrijven en doordat er veel administratieve operaties uitgevoerd moesten worden: het overzicht op de structuur van het programma raakte je daardoor kwijt. Blokschema’s maakten het juist mogelijk om die structuur en die blokken functionaliteit duidelijk aan te geven. Het grote nadeel van blokschema’s was vaak de inefficiëntie van de uiteindelijke programma’s; door ‘geraffineerd van de—vaak onbedoelde!—speciale eigenschappen van de machine gebruik te maken’13 was het mogelijk ‘uitgekookte “getructe” programma’s’14 te maken. Op een dergelijke manier optimum programmeren was geschikt voor het maken van standaard subroutines.
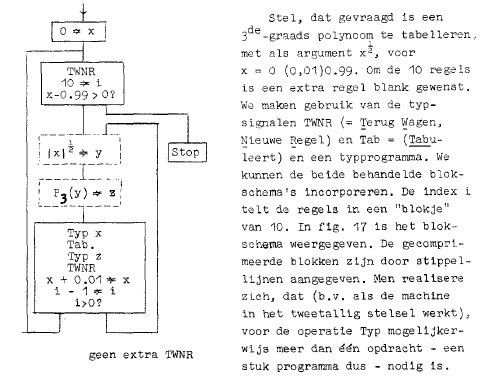
Door bepaalde conventies in acht te houden werden blokschema’s vereenvoudigd. Een blokschema bestond uit blokken, oftewel functionele eenheden, die je met lijnen met elkaar verbond. Een lijn kwam bovenaan een blok binnen en verliet het blok onderaan, pijlen waren dus overbodig. Een keuzemogelijkheid gaf je aan door een vraag te stellen onderaan in een blok met twee uitgangen. De linkeruitgang was dan het nee-geval en de rechteruitgang het ja-geval. Verder werd in deze cursus ook een symbool gebruikt voor toekenning van waarden aan variabelen. Aanroepen van subroutines, die in zichzelf al functionele eenheden waren, gaf je aan met een gestippeld blok. In de figuur hierboven is een voorbeeld gegeven van blokschema dat een programma voorstelt dat de \(3^{\textrm{de}}\)-graads polynoom tabelleert.
In de tweede cursus werd ook een zogenaamd verloopschema geïntroduceerd dat in de eerste cursus nog niet voorkwam. In een verloopschema kon je de volgorde aangeven waarin de aritmetische operaties werden uitgevoerd. Veelal was zo’n verloopschema bedoeld om een groot aantal vergelijkbare operaties weer te geven. Een dergelijk verloopschema kon je omzetten in een blokschema door de introductie van een teller en een iteratie. Zo’n programma was dan vaak langzamer dan het gestrekte programma waarin je alle operaties uitschreef. Het gestrekte programma nam weer wel meer geheugenruimte in beslag.
Het grootste deel van de rest van de cursus werd besteed aan subroutines van verschillende aard. Het nut van standaard subroutines, de herbruikbaarheid en daardoor het verminderen van fouten en programmeertijd, werd uitgelegd. Een aantal standaard subroutines werd uitgebreid besproken door verschillende manieren om dergelijke functies, zoals de sinus, het worteltrekken en het machtsverheffen, uit te werken tot blokschema’s.
Voordat administratieve subroutines en superprogramma’s werden besproken, verschoof de aandacht naar de kwaliteit van programma’s en subroutines. Eigenschappen zoals snelheid, schaling, controle en flexibiliteit werden besproken. De snelheidsbeperkende factor van een machine was over het algemeen het geheugen. Door de introductie van snel geheugen en een buffer was dit bij de ARMAC eigenlijk geen probleem meer. Schaling was het vermenigvuldigen van constanten en variabelen met geschikt gekozen schalingsfactoren waardoor ze een hanteerbare orde van grootte kregen. Als geen goed idee bestond over de orde van grootte dan moesten andere getalrepresentaties, zoals de drijvende komma, gebruikt worden.
Tot controle behoorden al die maatregelen die je als programmeur trof om er zeker van te zijn dat de door jouw programma verkregen resultaten overeenkwamen met de bedoelde resultaten. Ook hierbij gold dat deze controle steeds meer in handen van de machine kwam. Bij de ARMAC was er bijvoorbeeld een paritycheck in het geheugen ingebouwd, een extra bit zodat het aantal enen in een half woord plus een altijd oneven was. Bleek bij controle dat dit niet het geval was, dan stopte de machine.
Maar je moest als programmeur toch zelf ook controles inbouwen in je programma’s:
In tegenstelling tot het verleden is nu het stadium bereikt, dat de zwakste schakel in het proces niet meer de machine, maar – de programmeur is! En de programmeur doet er goed aan met behulp van het programma zichzelf te controleren.15
Bijvoorbeeld om het gebrek aan accuratesse bij het ponsen te verhelpen.
Flexibiliteit van een programma hield in dat het programma robuust was: dat na een machinefout of tijdens het testen het programma herstart kon worden. Maar ook het eenvoudig kunnen wijzigen van een programma was een onderdeel van de flexibiliteit. Sterker nog, zodra een programma hergebruikt kon worden, deed je er goed aan de flexibiliteit ervan in het oog te houden:
de moeilijkheid is dat veelal de wens naar voren zal komen een bestaand programma te gebruiken op een manier, die niet precies bedoeld was, voor een probleem, waarvoor het programme niet precies gemaakt was. De programmeur maakt het programma, d.w.z. een precieze formulering van het rekenschema: aan hem wordt overgelaten, rekening te houden met allerlei mogelijke nog niet geformuleerde eisen.16
Subroutines met een coördinerende taak werden administratieve subroutines genoemd, ze riepen andere subroutines aan en konden op verschillende manieren aangeroepen worden om de gewenste, iets verschillende, functionaliteit te verkrijgen. Als voorbeeld werden subroutines voor tabellatie en integratie genoemd.
Tenslotte werden zogenaamde superprogramma’s behandeld. De term “superprogramma” werd in de cursus gebruikt om die programma’s aan te duiden die de taak hadden om andere programma’s te onderzoeken, te interpreteren of op een andere manier met of op programma’s werken. Het doel van deze programma’s, zoals een invoerprogramma of een drijvende komma programma, was om het leven van de programmeur gemakkelijker te maken. Een ander voorbeeld was een zogeheten ladderprogramma dat iteraties automatisch uitschreef.
Overigens werd de term “superprogramma” niet gebruikt in de andere besproken rapporten, het was bedoeld om tijdens de cursus een bepaald soort programma te karakteriseren. In het hoofdstuk over superprogramma’s werd dan ook niet gesproken over hoe dergelijke programma’s gemaakt kunnen worden, enkel de mogelijkheden van superprogramma’s werden besproken. Superprogramma’s waren als het ware voorlopers van besturingssystemen, compilers, interpreters en andere tools. Deze superprogramma’s maakten, vanuit het perspectief van de gebruiker, onderdeel uit van het computersysteem, het waren systeemprogramma’s.
Een belangrijke klasse superprogramma’s was de klasse van het interpreterende programma: programma’s die
het objectprogramma wezenlijk kunnen interpreteren, d.w.z. met inachtneming van de werking van het objectprogramma.17
In de cursus werden drie verschillende soorten interpreterende programma’s onderscheiden: interpreters die machinecode in het geheugen interpreteerden, interpreters die objectcode (anders dan machinecode) in het geheugen interpreteerden en interpreters die objectcode vanuit de invoer omzette in machinecode instructies.
De eerste soort interpreterende programma’s vormden samen met de machine waarop het draaide een nieuwe machine die vergelijkbaar was met de originele machine.
[E]en pseudo-machine, die handelt als de echte machine, maar daar[b]ij nog voortdurend verslag uitbrengt van zijn handelingen als een neurotische patiënt aan de psychiater (nl. de programmeur). (…) Het interpreterende programma moet zelf een pseudo-machine bijhouden in de vorm van een aantal adressen gebruikt als pseudo-opdrachtteller, pseudo-rekenregister, pseudo-condities, enz.18
De tweede soort interpretatieve programma’s interpreteerde programma’s die al in het geheugen van de machine aanwezig waren maar niet in de machine code gesteld waren. Deze programma’s draaiend op een machine vormden een pseudo-machine met nieuwe functionaliteit, bijvoorbeeld het rekenen met drijvende komma. Omdat deze programma’s traag waren, was het van belang om te kunnen wisselen van interpretatieve modus naar niet-interpretatieve modus: een groot deel van een programma bestond uit administratieve handelingen, en die konden net zo goed op de echte machine uitgevoerd worden.
De laatste soort interpretatieve programma’s werkte op programma’s op ponsband. Deze programma’s konden op twee wijzen verwerkt worden: het programma werd vertaald naar een equivalent machine code programma of het de programmaregels en voert die uit19. Het invoerprogramma was het voorbeeld van de eerste verwerkingswijze. De programmeurscode werd omgezet in machinecode en het programma werd in het geheugen gezet waarna het uitgevoerd kon worden.
Het hoofdstuk over superprogramma’s werd besloten met:
In het algemeen kan men zeggen, dat een schier eindeloze hoeveelheid “kennis” in de superprogramma’s kan worden opgeslagen, zodat het converseren met de machine meer het karakter krijgt van het praten tot een collega in plaats van tegen een imbeciele slaaf.’20
Deze cursus gaf wel een inzicht in hoe er aan de Rekenafdeling over programmeren werd gedacht, maar het gaf geen inzicht in hoe er nu eigenlijk geprogrammeerd werd, hoe verschillende mensen met een probleem hebben zitten worstelen, wat de ontwikkelingscyclus was, hoe vaak er getest werd, hoe lang gemiddeld een programma was, enzovoorts. Deze cursus en rapporten geven een geïdealiseerd beeld van het programmeren, de dagelijkse gang van zaken blijft verborgen.
Literatuur
-
Dijkstra en Wijngaarden, ‘Programmeren voor automatische rekenmachines. Cursus 1955/56’, 1.↩︎
-
‘Notulen van de 14e Curatorenvergadering van het Mathematisch Centrum, gehouden op Donderdag 29 April 1954 in het gebouw van het Mathematisch Centrum’.↩︎
-
‘Jaarverslag Mathematisch Centrum’, 1954; ‘Jaarverslag Mathematisch Centrum’, 1955.↩︎
-
‘Jaarverslag Mathematisch Centrum’, 1956; ‘Jaarverslag Mathematisch Centrum’, 1958.↩︎
-
‘Notulen 5e Curatorenvergadering van het Mathematisch Centrum te Amsterdam op 11 Maart 1948 des namiddags om 2 uur in de kamer van de Wethouder van Onderwijs ten Stadhuize’, 1.↩︎
-
‘Toelichting nieuwe rekenapparatuur 4 maart 1963’, 3.↩︎
-
‘Notulen van de 49e vergadering van het Curatorium van de Stichting Mathematisch Centrum te Amsterdam, gehouden op donderdag 20 oktober 1966’, 4.↩︎
-
‘Jaarverslag Mathematisch Centrum’, 1957, 61–64.↩︎
-
Dijkstra en Wijngaarden, ‘Programmeren voor automatische rekenmachines. Cursus 1955/56’.↩︎
-
Dijkstra, ‘Functionele beschrijving van de ARRA’, 33.↩︎
-
Ibid.↩︎
-
Dekker, Dijkstra, en Wijngaarden, ‘Cursus programmeren voor automatische rekenmachines’, 20.↩︎
-
Ibid., 21.↩︎
-
Ibid.↩︎
-
Ibid., 79.↩︎
-
Ibid., 82.↩︎
-
Ibid., 103.↩︎
-
Ibid., 104.↩︎
-
Dit is dus eigenlijk het latere onderscheid tussen compilers en interpreters.↩︎
-
Dekker, Dijkstra, en Wijngaarden, ‘Cursus programmeren voor automatische rekenmachines’, 106.↩︎
