Inleiding

Verschillende onderzoekers hebben gepleit voor nieuw wetenschaps- en technologieonderwijs om onze kinderen beter voor te bereiden op hun deelname aan de moderne informatiesamenleving (Gravemeijer, 2009; Keulen, 2009; Léna, 2006; Millar & Osborne, 1998). In deze informatiesamenleving is het interpreteren, het representeren en het manipuleren van allerlei dynamische processen en systemen een belangrijke activiteit geworden. Zo kunnen we, bijvoorbeeld, door patronen in ons energieverbruik te analyseren, energie besparen. En door bedrijfsprocessen realtime te visualiseren kunnen we sneller gefundeerde beslissingen nemen. Om dit te kunnen doen, heb je echter een meer wiskundig begrip van verandering in deze dynamische processen en systemen nodig.

Deze wiskunde¹ wordt traditioneel onderwezen in de bovenbouw van havo/vwo en in het hoger onderwijs en staat bekend als wiskundige analyse of de differentiaal- en integraalrekening. De basis van wiskundige analyse is de algebra. Algebra is geen onderdeel van het curriculum Rekenen-Wiskunde op de basisschool. Dat maakt deze wiskundige analyse ongeschikt voor het basisonderwijs. Aan de andere kant biedt de moderne informatietechnologie jongere leerlingen de mogelijkheid om dynamische processen en systemen te onderzoeken, bijvoorbeeld met behulp van interactieve computersimulaties van dergelijke systemen en processen. Daarbij is het voor de leerlingen niet nodig om gebruik te maken van algebra (Kaput & Schorr, 2007; Stroup, 2002; Thompson, 1994). We noemen het onderwijzen van concepten uit de differentiaalrekening op de basisschool “primary calculus”.

Vanuit een constructivistisch perspectief op leren en het vergaren van kennis zijn we een design research project (Gravemeijer & Cobb, 2006) begonnen met de onderzoeksvraag: hoe kunnen we de differentiaalrekening onderwijzen op de basisschool?

Het traditionele onderwijs van de differentiaalrekening is sterk gebaseerd op de wiskundige definitie van de momentane snelheid als de limiet van de gemiddelde snelheid op een oneindig klein tijdsinterval. Laat de verandering van een grootheid worden beschreven met functie \(f\). De momentane snelheid waarmee die grootheid verandert op moment \(m\) is dan gedefinieerd als \(\lim\limits_{h \rightarrow 0}\frac{f(m + h) - f(m)}{h}\). Deze definitie suggereert dat het begrip van gemiddelde snelheid en het limiet concept voorwaardelijk zijn voor begrip van momentane snelheid. Dientengevolge wordt tijdens het onderwijzen van de traditionele differentiaalrekening de gemiddelde snelheid eerst onderwezen, gevolgd door het concept limiet. Daarna dienen de leerlingen een begrip van momentane snelheid op te bouwen door zich de gemiddelde snelheid op steeds kleinere intervallen voor te stellen. Als dat interval de lengte nul benadert, dan zeggen we dat de gemiddelde snelheid op dat interval de momentane snelheid benadert. Limiet is echter een zogenaamd threshold concept (Meyer & Land, 2003) in de wiskunde, het is moeilijk te begrijpen (Cornu, 1991; Doorman, 2005). Het is een van de meest pregnante problemen voor studenten tijdens het leren van de differentiaalrekening (Tall, 1993).

We vermoeden dat het concept limiet voor basisschoolleerlingen nog problematischer is, maar zowel limiet als momentane snelheid worden nauwelijks behandeld in de literatuur over het onderwijzen van concepten uit de wiskundige analyse aan jongere leerlingen. In die literatuur ligt de focus voornamelijk op het ontwikkelen van een meer kwalitatief begrip van snelheid (zoals in Stroup, 2002) of de focus gaat uit naar lineaire situaties (Kaput & Roschelle, 1998; Kaput & Schorr, 2007; Roschelle et al., 2000). Er zijn een klein aantal andere onderzoeken verricht die vanaf het begin voorbijgaan aan lineaire situaties (Ebersbach, Van Dooren, & Verschaffel, 2011; Galen & Gravemeijer, 2010; Saldanha & Thompson, 1998). In deze onderzoeken werd het concept momentane snelheid enkel impliciet behandeld als het al aan bod kwam en eventuele problematische aspecten werden niet besproken.

Basisschoolleerlingen hebben echter ook een intuïtief begrip van momentane snelheid. Het grootste deel van hun leven ervaren ze immers allerlei dynamische fenomenen, van het naar school fietsen tot het spelen van computerspellen. Ook in de geschiedenis van de ontwikkeling van het begrip momentane snelheid bestond zo’n intuïtief begrip veel eerder dan de nu standaard wiskundige definitie (Doorman, 2005). Rond 1335 definieerde Willem van Heytesbury zijn intuïtieve begrip van momentane voortbewegingssnelheid als:

‘a nonuniform or instantaneous velocity (…) is not measured by the distance traversed, but by the distance which would be traversed by such a point, if it were moved uniformly over such or such a period of time at that degree of velocity with which it is moved in that assigned instant.’ (uit: Heytesbury (1335) Regule solvendi sophismata, zoals geciteerd in (Clagett, 1959, pp. 235–237))

In een vorig deelstudie hebben we ervaring en kennis opgedaan over de voorkennis van concepten uit de differentiaalrekening bij leerlingen uit groep 7. Op basis van de resultaten van die deelstudie, Heytesburys intuïtieve definitie van momentane snelheid en andere bronnen hebben we een initieel hypothetisch leertraject opgesteld over het onderwijzen van de differentiaalrekening op de basisschool. Dit hypothetische leertraject vormde de basis van een ICT-rijke lessenserie over snelheden in de context van het vullen van glazen en flessen. Tijdens de uitvoering van deze lessenserie probeerden we basisschoolleerlingen een maat voor momentane snelheid to laten ontwikkelen zonder dat ze daarbij gebruik maken van het problematische limiet concept. Om inzicht te krijgen in hoeverre en hoe dit onderliggende hypothetisch leertraject het leren van momentane snelheid door basisschoolleerlingen ondersteunde, bespreken we de ontwikkeling, uitvoering en evaluatie van deze lessenserie.

Hypothetisch leertraject

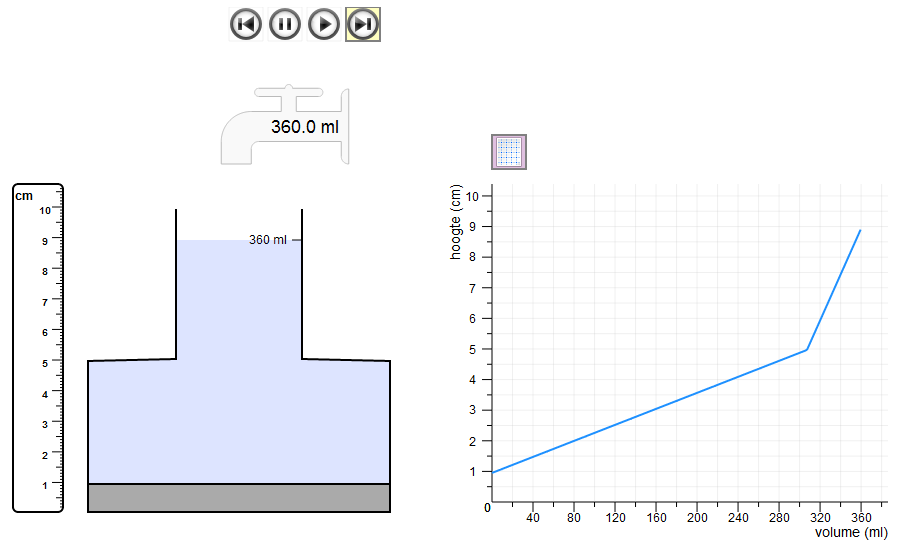
Leerlingen ontwikkelen hun begrip van momentane snelheid in een specifieke context op. We hebben gekozen voor de context van het vullen van glazen met water. Het is een eenvoudige context waarmee de leerlingen zeer vertrouwd zijn omdat ze zelf regelmatig glazen onder de kraan gevuld zullen hebben. Daarnaast is de verandering van de hoogte visueel duidelijk zichtbaar en kan eenvoudig gesimuleerd worden. Tot slot kan zo’n simulatie gekoppeld worden aan een grafiek doordat de hoogte van het water op de verticale as in de grafiek overeenkomt met de hoogte van het water in de simulatie.

Het hypothetisch leertraject bestaat uit twee delen: het verdiepen van het concept momentane stijgsnelheid in de context van het vullen van glazen en transfer van dat begrip naar snelheid in de context van het racen met speelgoedautootjes.

Momentane stijgsnelheid

Maatbekers maken

De docent introduceert de context van het vullen van glazen en flessen met een klassikale introductie over maatbekers. Leerlingen kennen maatbekers. Ze hebben maatbekers gebruikt in en om de keuken en op school zijn ze verschillende opdrachten tegengekomen over maatbekers, zoals verdeelproblemen, het rekenen met verschillende eenheden en het meten van volume. De maatbeker is een representatie van een bepaalde relatie tussen hoogte en volume. Leerlingen ervaren deze relatie door, achtereenvolgens, maatbekers van een longdrink glas, een cocktail glas en een Erlenmeyer te maken en onderzoeken. Hierdoor denken de leerlingen na over de relatie tussen hoogte en volume en hoe die te representeren in de vorm van een maatbeker.

De leerlingen herkennen de opdracht van het maken van een maatbeker van het longdrink glas als een verdeelprobleem waarmee ze bekend zijn. Met behulp van de vier gegeven maatstreepjes delen de leerlingen de maatbeker op in vijf gelijke stukken. De leerlingen realiseren zich dat in van deze stukken het volume steeds met dezelfde hoeveelheid toeneemt. De maatbeker wordt een discrete representatie van deze relatie tussen hoogtestijging per stuk en de daarbij horende toename van het volume.

Als de leerlingen vervolgens een maatbeker maken van het cocktail glas, verwachten we dat de meeste leerlingen door de zogenaamde lineariteitsillusie het glas op vergelijkbare wijze opdelen in gelijke stukken. Het evalueren van hun maatbeker door het simuleren van het vullen van het cocktail glas zet de leerlingen aan tot het nader bestuderen van de relatie tussen hoogte en volume weergegeven in de maatbeker. Gedurende de simulatie zien de leerlingen dat het water in het begin heel snel stijgt, maar dat daarna de snelheid steeds afneemt. Ze zien dat het opdelen van het cocktail glas in gelijke stukken niet kan kloppen. Dit nodigt de leerlingen uit om hun maatbeker te verbeteren en daarbij ontdekken ze een nieuw patroon van verandering: hoe breder het glas, hoe dichter de maatstreepjes bij elkaar staan. De maatbeker wordt zo een discrete representatie van de relatie tussen hoogte, volume en de breedte van het glas.

Voortbouwend op deze nieuwe relatie, verwachten we dat de leerlingen vervolgens een maatbeker van de Erlenmeyer maken die overeenkomt met het patroon van verandering zoals die zichtbaar is in de correcte maatbeker van de Erlenmeyer. Bij het evalueren van hun maatbeker zien de leerlingen dat hun maatbeker niet correct is omdat het welhaast onmogelijk is om met enkel een kwalitatief begrip van de relatie tussen hoogte, volume en de breedte van het glas de maatstreepjes precies op de juiste plek te zetten. We verwachten dat de leerlingen zich ondanks deze afwijkingen realiseren dat ze het patroon van verandering goed voorspeld hadden. Dit ondersteunt hun ontwikkelende begrip van de relatie tussen hoogte, volume en de breedte van het glas. Tegelijkertijd wordt ook de kwantitatief relatie tussen hoogte en volume geproblematiseerd omdat de leerlingen niet in staat zijn om een precieze maatbeker te maken zonder gebruik te maken van de simulatie.

Snelheid meten

Gebruik makend van hun begrip van de relatie tussen hoogte, volume en breedte van het glas kunnen de leerlingen de stijgsnelheid in een glas karakteriseren. De leerlingen zijn zich bewust van het verschil van de stijgsnelheid in de drie glazen. Waar het water in het longdrink glas stijgt met een constante snelheid, doet het dat nadrukkelijk niet in de andere twee glazen. Door de stijgsnelheid in de drie glazen te vergelijken, worden de leerlingen zich bewust van de relatie tussen (hoogte), volumetoename, breedte van het glas en de stijgsnelheid: hoe breder het glas, hoe langzamer het water stijgt. Dit maakt ook de weg open om de stijgsnelheid te relateren aan de verandering van hoogte van het waterpeil en het bijbehorende volume.

We verwachten dat de leerlingen die deze relatie ontwikkelen het cocktail glas aanduiden als het snelste glas omdat dit glas het smalst is in de punt. Omdat dit glas aan de top ook het breedst is, verwachten we ook dat dit discussie oplevert: het cocktail glas zowel het snelst als het langzaamst. Tijdens deze discussie realiseren de leerlingen zich dat er in het cocktail glas en de Erlenmeyer geen sprake is van een enkele snelheid, terwijl in het longdrink glas die snelheid constant is.

Longdrink glas

We verwachten dat leerlingen in staat zijn om de constante snelheid in het longdrink glas te bepalen. Ze begrijpen snelheid als een verhouding tussen afstand, in dit geval de hoogtestijging, en periode. Leerlingen kennen de eenheden zoals cm/sec of km/uur voor het uitdrukken van snelheden. Leerlingen bedenken dat de snelheid te bepalen is door te meten hoe lang het duurt voordat het glas is gevuld.

Met behulp van de computersimulatie van het vullen van het longdrink glas meten de leerlingen op verschillende tijdstippen de hoogte van het water. We ondersteunen de leerlingen bij het bepalen van de stijgsnelheid door hen dit stapsgewijs te laten doen: de leerlingen vullen een meettabel in, maken daarvan een grafiek om een overzicht van het gehele vulproces te krijgen, om op basis van die grafiek vervolgens de stijgsnelheid te berekenen door de hoogtestijging te delen door de tijd.

We verwachten dat deze stappen leerlingen helpen bij het bepalen van de stijgsnelheid en het beter begrijpen van het vullen van het longdrink glas. Eventuele meetfouten komen bovendrijven bij het tekenen van een grafiek. Leerlingen verachten een rechte schuine lijn als een grafiek en afwijkingen van een rechte lijn zullen de leerlingen aanzetten tot reflectie op de meetwaarden. Tegelijkertijd verwachten we dat sommige leerlingen de bodem meetellen bij het bepalen van de stijgsnelheid, terwijl andere leerlingen dat niet zullen doen. Deze verschillen noopt tot discussie over het verschil tussen hoogte en hoogteverandering en de relatie daarvan tot de stijgsnelheid.

Leerlingen zijn vertrouwd met (voortbewegings)snelheid in termen van afgelegde weg per tijdseenheid (cm/sec). We verwachten dat leerlingen hierdoor teruggrijpen op hun intuïtieve kennis van deze “gewone” snelheid bij het bestuderen van de stijgsnelheid. De eenheid cm/sec voor de stijgsnelheid is niet handig omdat de tijd van het vullen afhangt van de snelheid waarmee het water uit de kraan stroomt. Hierdoor kan het voorkomen dat in een situatie met twee dezelfde longdrinkglazen die gevuld worden door twee verschillende kranen de stijgsnelheid in dezelfde glazen niet dezelfde is. Na bestudering van zo’n situatie waarin het water in twee dezelfde glazen stijgt met een verschillende snelheid verwachten we dat leerlingen tijdens een discussie over deze situatie erkennen dat de grootheid tijd het probleem is en dat ze vervolgens willen zoeken naar een betere maat voor de stijgsnelheid. In een vorig experiment hebben we geleerd dat leerlingen op zich geen moeite hebben met een snelheidsmaat in termen van hoogte en volume (cm/ml). We ondersteunen de leerlingen bij het selecteren van deze nieuwe eenheid voor de stijgsnelheid.

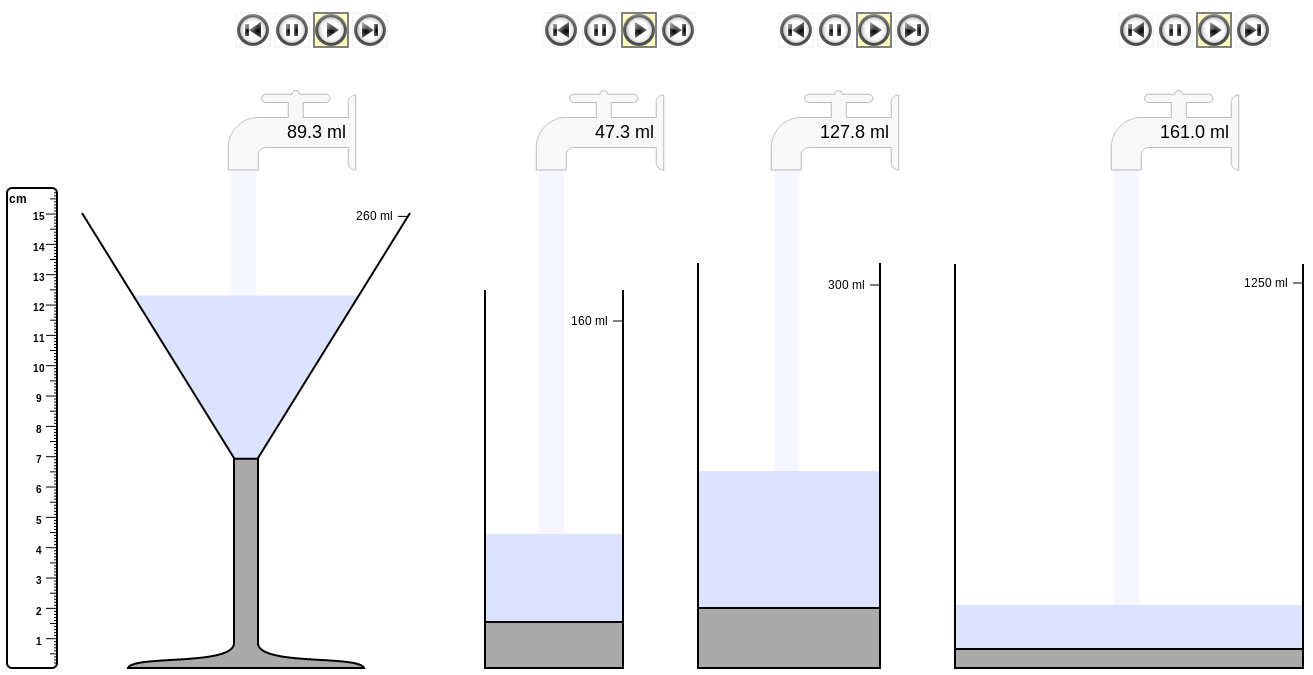
Cocktail glas

Om het probleem van meerdere stijgsnelheden in een glas te introduceren, krijgen de leerlingen de opdracht om de stijgsnelheid van een vaas te bepalen. Deze vaas bestaat uit twee delen: een breed onderste gedeelte met een smaller bovenste gedeelte. De leerlingen gaan hiermee aan de slag zoals ze dat bij het bepalen van de stijgsnelheid van het longdrink glas deden: meten, grafiek tekenen, om vervolgens daarmee de stijgsnelheid te bepalen.

Deze opdracht is problematisch voor de leerlingen omdat het niet precies past in hun model van stijgsnelheid bepalen door begin- en eindtoestand te vergelijken. Gebruik makend van dezelfde methode om de stijgsnelheid te bepalen, tekenen de leerlingen een rechte lijn als de grafiek en bepalen op basis daarvan een snelheid. Bij het vergelijken van hun grafiek met die van de simulatie zien ze dat de laatste bestaat uit twee rechte lijnen die weliswaar begint en eindigt op dezelfde plaats als hun getekende rechte lijn, maar die verder niet overeenkomt. De leerlingen realiseren zich dat de snelheid die ze hebben bepaald de gemiddelde snelheid is, maar dat die niet overeenkomt met de snelheid waar dan ook in de vaas. Dit nodigt de leerlingen uit om de stijgsnelheid te bepalen in zowel het onderste als het bovenste stuk van de vaas, waarbij elk stuk wel past in hun model van stijgsnelheid.

Maar dit model past niet meer voor het bepalen van de stijgsnelheid van het cocktail glas. De leerlingen weten dat de snelheid verandert van heel snel tot heel langzaam. Ze weten dat de grafiek niet een rechte lijn zal zijn. Toch verwachten we dat leerlingen de grafiek tekenen als een rechte lijn of met behulp van meerdere rechte lijnstukjes omdat de leerlingen niet beter weten dan dat grafieken rechte lijnen zijn. We verwachten dat leerlingen de gemiddelde snelheid gaan bepalen omdat dat past bij hun model van stijgsnelheid. Tegelijkertijd verwachten we dat de leerlingen onderkennen dat deze gemiddelde snelheid geen goede benadering van de snelheid in het cocktail glas is. De vloeiende kromme die de computer simulatie tekent, ondersteunt het vermoeden van de leerlingen dat de snelheid continue verandert. Leerlingen gaan beseffen dat op elk moment de snelheid anders is.

Longdrink glas als maat voor momentane stijgsnelheid in het cocktail glas

We vinden in de intuïtieve definitie van momentane voortbewegingssnelheid van Heytesbury (1335)² een heuristiek voor het ontwikkelen van een begrip van momentane stijgsnelheid in het cocktail glas. Parafraserend en vertaald naar de context van het vullen van glazen:

De snelheid waarmee het water stijgt in het cocktail glas op hoogte 9.4 cm is gelijk aan de snelheid waarmee het water zou stijgen in een longdrink glas dat even breed is als het cocktail glas op hoogte 9.4 cm.

We willen dat de leerlingen het longdrink glas gaan zien als een maat voor de momentane snelheid in het cocktail glas. Leerlingen begrijpen dat de stijgsnelheid afhangt van de breedte van het glas en, door het cocktail glas naast enkele longdrink glazen met verschillende breedte te plaatsen, we verwachten dat leerlingen aan kunnen geven op welke hoogte het water even snel stijgt in het cocktail glas als in een bepaald longdrink glas. Namelijk als ze even breed zijn. Leerlingen zien in dat ze zo op elke hoogte de stijgsnelheid in het cocktail glas kunnen bepalen door een longdrink glas te bedenken dat even breed is als het cocktail glas op die hoogte. De leerlingen begrijpen de stijgsnelheid van het cocktail glas als de stijgsnelheid in een opeenvolging van longdrink glazen van zo smal als in de punt tot zo breed als de top van het cocktail glas.

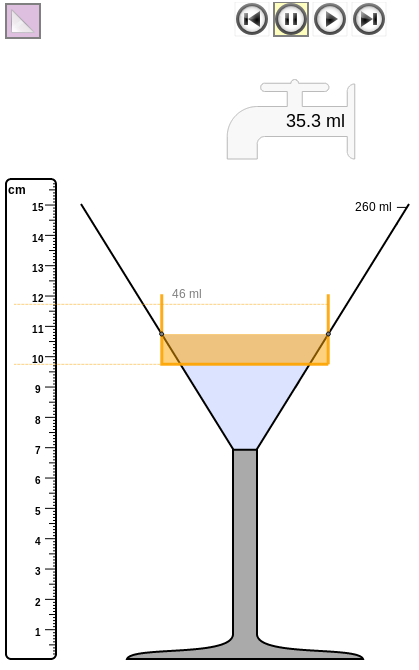
Met behulp van een computertool die een “denkbeelding” longdrink glas bovenop het cocktail glas tekent, kunnen leerlingen de momentane snelheid bepalen. Leerlingen zien de momentane snelheid op een bepaalde hoogte als de stijgsnelheid die het glas zou hebben als het een longdrink glas was met dezelfde breedte. De stijgsnelheid in het longdrink glas staat model voor de stijgsnelheid op een moment.

Transfer van momentane snelheid

Verbinden longdrink glas en raaklijn

Dit begrip van momentane stijgsnelheid is niet direct te vertalen naar begrip van momentane snelheden in andere contexten: daar spelen longdrink glazen immers geen rol. We zien de grafiek echter als medium om leerlingen dit begrip te laten abstraheren zodanig dat ze dit ook in andere contexten kunnen gebruiken. Net zoals het longdrink glas als maat voor de snelheid in het cocktail glas was, willen we dat leerlingen gaan inzien dat de grafiek van het longdrink glas als maat voor de snelheid in de grafiek van het cocktail glas kan dienen. Daartoe hebben we het “denkbeeldige” longdrink glas gekoppeld aan de raaklijn aan de grafiek.

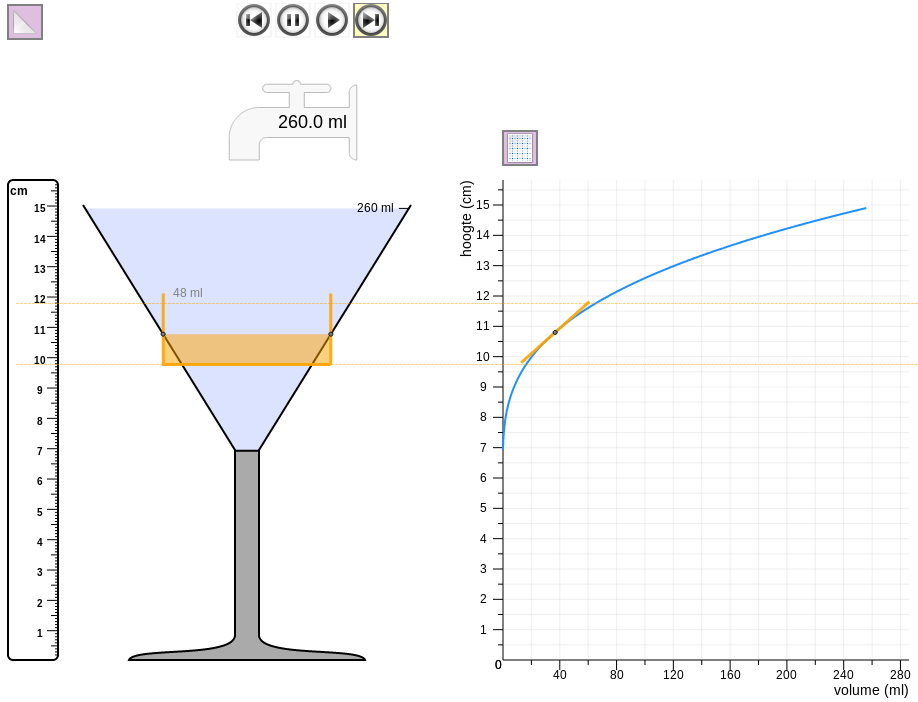
De leerlingen herkennen de gele rechte lijn als de grafiek van het longdrink glas en koppelen dat aan het longdrink glas als maat voor de momentane snelheid. Net zoals het longdrink glas precies op een moment even breed is als het cocktail glas, zo lopen de grafieken van het longdrink glas en het cocktail glas gelijk op dat punt. De leerlingen weten hoe de snelheid samenhangt met de grafiek van het longdrink glas: ze hebben dat gebruikt om de totale hoogtestijging en bijbehorende toename in volume te vinden bij het bepalen van de stijgsnelheid van het longdrink glas.

Raaklijn in een punt als maat voor de snelheid op een moment

Door deze koppeling tussen longdrink glas en rechte lijn te observeren op verschillende punten, gaan de leerlingen de steilheid van de lijn zien als een indicatie van de stijgsnelheid. Hoe steiler de lijn, hoe sneller het water stijgt. Leerlingen realiseren zich dat de steilheid van de grafiek van het cocktail glas een indicatie is van de stijgsnelheid.

Om van de grafiek van het denkbeeldige longdrink glaasje een meer algemene raaklijn te maken, verbreken we de expliciete koppeling tussen longdrink glaasje en grafiek van het longdrink glaasje. Leerlingen kunnen nu enkel nog met behulp van de grafiek en de raaklijn aan die grafiek de stijgsnelheid bepalen. Langzaamaan gaan de leerlingen minder denken in termen van de breedte van het longdrink glas, maar in termen van de steilheid van de raaklijn.

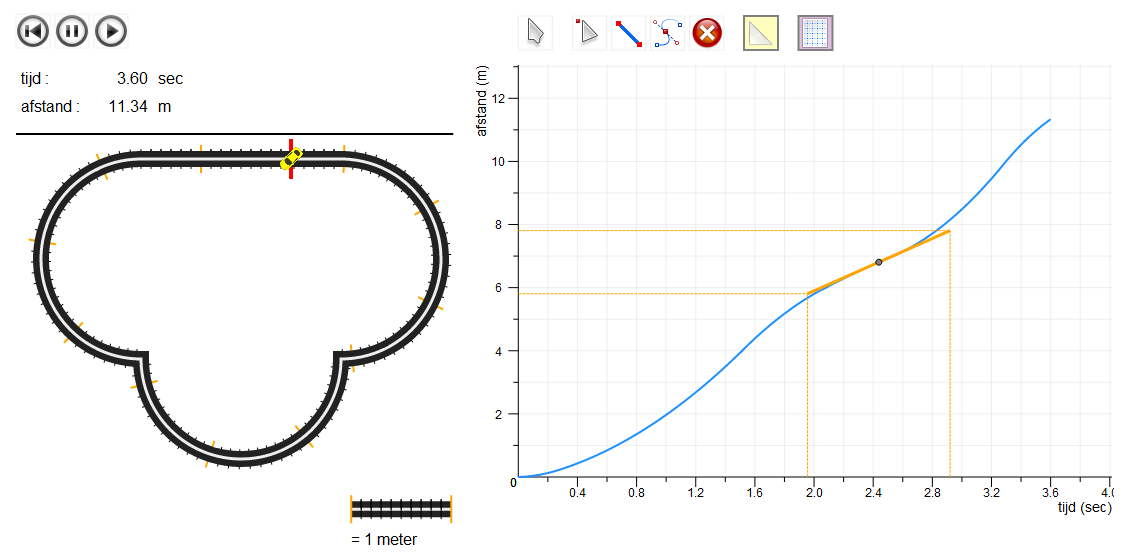
We verwachten dat leerlingen bij het zien van een grafiek zien van het racen met een speelgoedauto ook hier de steilheid van de grafiek koppelen aan de snelheid. Dit stelt de leerlingen in staat om de snelheid in deze situatie te onderzoeken. Leerlingen realiseren zich dat de raaklijn in deze grafiek een race voorstelt waarin de auto met constante snelheid doorrijdt maar dat de snelheid van de auto tijdens de race continue verandert.

Door de overeenkomsten en verschillen tussen de snelheid in deze situatie en die van het vullen van glazen te onderzoeken, gaan de leerlingen denken over momentane snelheid in termen van steilheid van de grafiek.

Uitvoering en evaluatie

Uitvoering lessenserie

We hebben de lessenserie uitgetest in een gemengde Leonardo groep 7/8 van een basisschool in Eindhoven. Gedurende de uitvoering deden ook vier leerlingen van de gewone, niet-hoogbegaafde groep 7/8 mee. Deze leerlingen presteerden boven gemiddeld in wiskunde en werden regelmatig uitgenodigd om met projecten uit de Leonardo groep mee te doen. Alles bij elkaar deden 15 jongens en 10 meisjes mee. Niet alle leerlingen deden met elke les mee door omstandigheden zoals ziekte en toetsen. Er waren altijd meer dan 15 leerlingen in de les. De jongste leerling was net 11 jaar geworden en de oudste 13 jaar (gemiddelde leeftijd = 11.52 jaar; σ = 0.586 jaren). De lessenserie bestond uit 5 lessen die op 5 verschillende dagen werden gegeven, gescheiden door 4 to 7 dagen. We probeerden voor en na elke les een voor- en nabespreking te houden met de docent, maar de tweede en vijfde les konden niet in een aparte bijeenkomst worden voorbesproken en de vierde les niet nagesproken. We waren wel altijd in staat om gedurende en direct na afloop van de les die les kort te bespreken. De docent had jarenlange ervaring in het basisonderwijs en vanaf de oprichting van de Leonardoafdeling drie jaar terug werkte ze in de gemengde Leonardo groep 7/8.

De leerlingen hadden geen extra verdieping van snelheid gehad ten opzichte van het standaardcurriculum. Volgens dat curriculum dienen leerlingen te kunnen rekenen met de bekende snelheidseenheden zoals km/uur en cm/sec[SLO (2006), pagina 12; Tule2009a]. Daarnaast adviseert het Nationaal expertisecentrum leerplanontwikkeling (SLO) om snelheid te behandelen als een verhouding en leerlingen te laten werken met situaties waarin gemiddelde snelheid en snelheidverschillen een rol spelen (Buijs, Klep, & Noteboom, 2008, pagina’s 40, 63, 171). Snelheid in het curriculum heeft verder weinig van doen met momentane snelheid zoals beschreven in het hypothetisch leertraject.

Ook wat betreft grafieken hadden deze Leonardoleerlingen weinig tot geen extra ervaring opgedaan. De weinige grafieken die ze op school tegenkwamen, waren rechte lijnen.

Dataverzameling en interpretatie

We hebben alle lessen en bijeenkomsten met de docent op video opgenomen. De leerlingen stuurden hun werk in via een interactief on-line werkblad. Onze analyse begon met het tabuleren van de antwoorden van de leerlingen, het transcriberen van de klassediscussies en, vervolgens, het in chronologische volgorde toevoegen van de antwoordtabellen aan de transcripties. Deze verrijkte transcripties vormden de basis voor thematische beschrijvingen van de data waaruit we twee thema’s selecteerden om nader te onderzoeken: “kwalitatief begrip van momentane snelheid” en “kwantitatief van momentane snelheid”. We interpreteerden de overgang van het redeneren over gemiddelde snelheid in de derde les naar redeneren over momentane snelheid in de vierde les als een sleutelmoment. We vroegen ons af: Hoe ontwikkelde het begrip over snelheid van de leerlingen van gemiddelde snelheid naar mommentane snelheid?

We beantwoorden deze vraag door te proberen te begrijpen hoe het begrip over snelheid van de leerlingen zich ontwikkelde gedurende lessen drie en vier en we illustreren ons begrip met de tijdens deze lessen verzamelde gegevens. Door middel van deze verrijkte beschrijving kregen we inzicht in hoeverre de leeromgeving de leerlingen ondersteunden bij het ontwikkelen van begrip van momentane snelheid. We interpreteerden deze transitie van gemiddelde naar momentane snelheid en de leeromgeving door gebruik te maken van een drievoudige classificatie van continue en discreet redeneren die door Castillo-Garsow (2012) werd geïntroduceerd. Deze classificatie bouwt voort op een classificatie van Bassok & Olseth (1995) waarin methoden en oplossingen worden geclassificeerd als of discreet van aard of continue van aard. Naast methoden en oplossingen classificeert Castillo-Garsow (2012) ook het redeneren waarmee leerlingen met die methoden tot oplossingen komen in termen van discreet en continue. Zij introduceerde daarvoor de termen “chunky” en “smooth” om het redeneren over snelheid bij leerlingen te beschrijven. Sommige leerlingen begrijpen snelheid als essentieel “chunky” van aard, dat wil zeggen, als de gemiddelde snelheid op een interval. Het interval kan kleiner gemaakt worden, maar deze leerlingen hebben moeite met het begrijpen van snelheid als een continue verandering. Leerlingen die snelheid begrijpen als essentieel “smooth”, daarentegen, begrijpen snelheid als momentane snelheid, maar kunnen snelheid ook begrijpen in termen van een gemiddelde snelheid over een interval.

Wij gebruiken dit onderscheid tussen “smooth” en “chunky” om de transitie van de leerlingen van gemiddelde snelheid naar momentane snelheid nader te bekijken. Door naar de verrijkte beschrijving te kijken met de lens van de drievoudige classificatie van continue en discrete problemen, methoden, redeneren en oplossingen kunnen we proberen om het rederen van leerlingen over snelheid beter te begrijpen.

Resultaten

Discrete leeromgeving

Uit de analyse blijkt dat gedurende de eerste drie lessen feitelijk een “chunky” manier van denken werd gepromoot door zowel de opzet van de verschillende taken als door de docent. De taken waren bedoeld om de leerlingen verandering in de grootheden volume en hoogte te laten coördineren, maar tegelijkertijd zorgde het er ook voor dat leerlingen over snelheid gingen nadenken in termen van maatstreepjes, hoogteverschillen en intervallen. Dat “chunky” beeld van snelheid van de leerlingen werd versterkt door de docent tijdens klassediscussies over de stijgsnelheid in het longdrink glas. Ze stimuleerde de leerlingen om over het bepalen van de stijgsnelheid na te denken, zonder in te gaan op wat snelheid nou eigenlijk betekende voor haar of de leerlingen. Dus, toen de taak verschoof van het bepalen van de stijgsnelheid in het longdrink glas naar het bepalen van de stijgsnelheid in het cocktail glas, interpreteerden de leerlingen deze niet-lineaire situatie in termen van het “chunky” beeld van verandering. Hierdoor hadden ze moeite om dat perspectief te rijmen met de continue veranderende waterhoogte. Ze uitten hun ontwikkelende begrip van momentane snelheid dan ook in termen van gemiddelde snelheid.

Procedurele kennis

Aan de einde van de derde les en het begin van de vierde les werd het longdrink glas geïntroduceerd als een maat voor de momentane snelheid in het cocktail glas. Na enige docent-gestuurde oefening met het longdrinkmeetgereedschap leken de leerlingen er goed mee overweg te kunnen. Leerlingen waren in staat om interessante punten op het glas aan te wijzen waar het water het snelst of het langzaamst steeg en met behulp van het longdrinkmeetgereedschap konden ze de bijbehorende stijgsnelheid bepalen. Op vergelijkbare wijze waren de leerlingen in staat om de snelheid van het speelgoedautootje te bepalen met behulp van het raaklijnmeetgereedschap nadat de context van het vullen van glazen was ingeruild voor die van het racen met speelgoedautootjes.

Maar transfer van begrip van de ene naar een andere context is niet triviaal (Herbert & Pierce, 2011). Tijdens de vierde les lag de focus van de klassediscussies voornamelijk op hoe de momentane snelheid bepaald kon worden met behulp van het raaklijnmeetgereedschap. Wederom werd de idee van een momentane snelheid niet besproken. We vermoeden dat de vaardigheid die de leerlingen ten toon spreidden met het gebruik van deze gereedschappen om de momentane snelheid te bepalen voornamelijk procedureel was, en niet zozeer een uiting van een dieper begrip van momentane snelheid.

Transfer

Het idee om een denkbeeldig longdrink glas te gebruiken als maat voor de momentane snelheid is uitermate geschikt voor de context van het vullen van glazen. Leerlingen zijn zeer bekend met deze context, ze vullen immers zelf regelmatig glazen en flessen, en het is eenvoudig om te begrijpen. Daarbovenop is het afbeelden van een denkbeeldig longdrink glaasje bovenop een ander glas een krachtig stuk denkgereedschap. Het mentale model van stijgsnelheid in het longdrink glas van leerlingen werd gekoppeld aan het mentale model van stijgsnelheid in het cocktail glas dat de leerlingen aan het ontwikkelen waren. Tegelijkertijd is het een idee en gereedschap dat zich niet gemakkelijk laat vertalen naar andere contexten. En het is niet gemakkelijk om vergelijkbare ideeën te vinden voor dergelijke andere contexten. Om transfer van begrip mogelijk te maken, moeten de leerlingen hun begrip op een of andere manier generaliseren. Zeker ook omdat het begrip van een leerling van snelheid afhankelijk is van de representatie die gebruikt wordt (Herbert & Pierce, 2011). Wij hebben ervoor gekozen deze generalisatie te ondersteunen via de grafiek en de raaklijn aan die grafiek. Leerlingen hebben echter moeite met grafieken (Ainley, Pratt, & Nardi, 2001; Garcia & Cox, 2010; Leinhardt, Zaslavsky, & Stein, 1990) en basisschoolleerlingen hebben nagenoeg geen ervaring met grafieken anders dan met “chunky” lijngrafieken. Dit heeft waarschijnlijk ook bijgedragen aan het beperkt blijven van verdieping van begrip van momentane snelheid.

Aan de andere kant waren de leerlingen wel in staat om de momentane snelheid te bepalen, er oppervlakkig over te praten en redeneren zonder het treshold concept limiet te gebruiken. Verschillende leerlingen lieten tekenen van “smooth” redeneren zien, maar veel leerlingen vielen ook steeds terug op het “chunky” perspectief. Dit gebeurde ook wanneer ze op een kwalitatieve manier over berekende snelheden probeerden te spreken. Deze mix van procedurele kwantificatie en persistente intuïtieve kennis, zoals het interpreteren van een snelheid als een verhouding tussen afstand of hoogte en tijd, past bij David Perkins beeld van conceptueel moeilijke kennis (Perkins, 2006). Hij stelt onderzoeksgericht onderwijs met kwalitatieve problemen voor om leerlingen de betekenis van concepten te laten onderzoeken in plaats van enkel kwantificatieprocedures aan te leren (Perkins, 2006).

In hoeverre ondersteunde de HLT het leren van momentane snelheid?

Terugkijkend op het hypothetische leertraject na de uitvoering en analyse van de lessenserie, moeten we concluderen dat we op basis van dit experiment niet kunnen beoordelen in hoeverre het hypothetische leertraject het leren van momentane snelheid door basisschoolleerlingen ondersteunde. Ja, de leerlingen geven blijk van vaardigheid met de geïntroduceerde denkgereedschappen om de momentane snelheid te bepalen. En leerlingen geven blijk over een dynamische situatie te kunnen redeneren aan de hand van de grafiek. Maar het is onduidelijk in hoeverre deze kennis procedureel of conceptueel van aard is. Deze duidelijkheid had naar voren moeten komen tijdens de klassediscussies. Maar tijdens de klassediscussies kwamen nagenoeg geen uitingen naar voren ter ondersteuning van een conceptuele ontwikkeling. En dat werd veroorzaakt doordat de klassediscussies niet vruchtbaar bleken voor conceptuele discussie.

Ogenschijnlijk leken de leerlingen blijk te geven van dieper begrip van momentane snelheid door hun vaardigheid met de geïntroduceerde denkgereedschappen, grafieken, en situaties. Voor de docent leken de leerlingen inderdaad de leerdoelen te bereiken. De leeromgeving bood weinig tot geen ondersteuning voor het voeren van conceptuele discussies door een focus op het uitvoeren van taken en het gebrek aan actief modelleren door de leerlingen. Dit gaf de docent weinig gereedschap in handen om het begrip van de leerlingen te beoordelen anders dan hun vaardigheid bij de opdrachten en het gebruik van de gereedschappen. Tegelijkertijd koos de docent ervoor om tijdens de lessen geen inhoudelijke discussie met leerlingen aan te gaan en hun begrip van snelheid te beoordelen, maar om te focussen op het ontwikkelen van de vaardigheid het bepalen van de momentane snelheid bij de leerlingen. Zonder daarbij ook een inhoudelijke discussie te voeren of anderszins inzicht proberen te krijgen in de mentale beelden over snelheid van de leerlingen, stelt dat ons echter niet in staat om de conceptuele ontwikkeling van de leerlingen te volgen.

Vervolg

We denken nog steeds dat het onderliggende idee, namelijk het longdrink glas als maat voor momentane snelheid in andere glazen, vruchtbaar is bij het ontwikkelen van een dieper begrip van momentane snelheid. We hebben geleerd dat een discrete leeromgeving niet ideaal is voor het ontwikkelen van begrip van een continue concept. We gaan in een vervolg experiment een leeromgeving opbouwen vanuit een “smooth” perspectief dat continue denken nadrukkelijk ondersteunt. De onderliggende vraag is hierbij: was het chunky denken van de leerlingen het resultaat van discrete leeromgeving of is chunky denken een essentiële stap in de ontwikkeling van begrip van een “smooth concept” zoals momentane snelheid? Of, anders geformuleerd: kunnen leerlingen begrip van een smooth concept ontwikkelen zonder daarbij eerst snelheid te begrijpen vanuit een chunky perspectief?

Literatuur